1. voorkennis
De vergelijking ax+by=c
De grafiek van de lineaire vergelijking ax+by=c is een rechte lijn.
De lijn 3x-5y=30 gaat door de punten (10,0) en (0,-6). Door y vrij te maken kan je de richtingscoëfficient vinden. Je kunt 3x-5y=30 ook schrijven als y=$\frac{3}{5}$x-6.
De vergelijking $\Large\frac{x}{a}+\Large\frac{y}{b}$=1
De vergelijking $\large\frac{x}{a}+\large\frac{y}{b}$=1 heet de assenvergelijking van een lijn. De lijn snijdt de assen in de punten (a,0) en (0,b).
De lijn door (10,0) en (0,-6) heeft als vergelijking $\large\frac{x}{10}+\large\frac{y}{-6}$=1. Ofwel 3x-5y=30.
Cosinusregel
In een willekeurige driehoek ABC geldt:
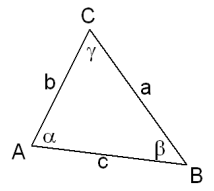
- $a^{2}=b^{2}+c^{2}-2bc·cos(\alpha)$
- $b^{2}=a^{2}+c^{2}-2ac·cos(\beta)$
- $c^{2}=a^{2}+b^{2}-2ab·cos(\gamma)$
Voorbeeld
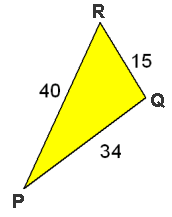
- Bereken $\angle P$ in hele graden.
Uitwerking
$
\begin{array}{l}
15^2 = 40^2 + 34^2 - 2 \cdot 40 \cdot 34 \cdot \cos \angle P \\
225 = 1600 + 1156 - {\rm{2720}} \cdot \cos \angle P \\
225 = {\rm{2756 - 2720}} \cdot \cos \angle P \\
2720 \cdot \cos \angle P = {\rm{2531}} \\
\cos \angle P = \frac{{{\rm{2531}}}}{{2720}} \\
\angle P \approx 21^\circ \\
\end{array}
$