4. stelsels en matrices
Oplossen van stelsels met behulp van matrices
Een matrixvermenigvuldiging:
$\left({\begin{array}{*{20}c}1&{-4}\\2&3\\\end{array}}\right)\left({\begin{array}{*{20}c}x\\y\\\end{array}}\right)=\left({\begin{array}{*{20}c}8\\5\\\end{array}}\right)$
Uitwerken geeft:
$\left\{\begin{gathered}x-4y=8\\2x+3y=5\\\end{gathered}\right.$
Het stelsel hierboven kan je noteren als:
$\left({\left.{\begin{array}{*{20}c}1&{-4}\\2&3\\\end{array}}\right|\begin{array}{*{20}c}8\\5\\\end{array}}\right)$
De matrix $\left({\begin{array}{*{20}c}1&{-4}\\2&3\\\end{array}}\right)$ heet de coëfficiëntenmatrix van het stelsel.
De matrix $\left({\left.{\begin{array}{*{20}c}1&{-4}\\2&3\\\end{array}}\right|\begin{array}{*{20}c}8\\5\\\end{array}}\right)$ heet de aangevulde matrix van het stelsel.
Elk stelsel lineaire vergelijkingen is te noteren als een matrix. Zo hoort bij het stelsel:
$\left\{\begin{gathered}x+2y+3z=0\\3x-y+4z=3\\2x+5y-z=15\\\end{gathered}\right.$
de matrix:
$\left({\left.{\begin{array}{*{20}c}1&2&3\\3&{-1}&4\\2&5&{-1}\\\end{array}}\right|}\right.\left.{\begin{array}{*{20}c}0\\3\\{15}\\\end{array}}\right)$
Noem de rijen van de matrix $R_1$, $R_2$ en $R_3$. Je kunt het stelsel dan zo oplossen:
-
Trek $3R_1$ af van $R_2$ en trek $2R_1$ af van $R_3$
$\left({\left.{\begin{array}{*{20}c}1&2&3\\3&{-1}&4\\2&5&{-1}\\\end{array}}\right|}\right.\left.{\begin{array}{*{20}c}0\\3\\{15}\\\end{array}}\right)\to\left({\left.{\begin{array}{*{20}c}1&2&3\\0&{-7}&{-5}\\0&1&{-7}\\\end{array}}\right|}\right.\left.{\begin{array}{*{20}c}0\\3\\{15}\\\end{array}}\right)$ -
Tel $7R_3$ op bij $R_2$
$\left({\left.{\begin{array}{*{20}c}1&2&3\\0&{-7}&{-5}\\0&1&{-7}\\\end{array}}\right|}\right.\left.{\begin{array}{*{20}c}0\\3\\{15}\\\end{array}}\right)\to\left({\left.{\begin{array}{*{20}c}1&2&3\\0&0&{-54}\\0&1&{-7}\\\end{array}}\right|}\right.\left.{\begin{array}{*{20}c}0\\{108}\\{15}\\\end{array}}\right)$ -
Deel $R_2$ door $-54$
$\left({\left.{\begin{array}{*{20}c}1&2&3\\0&0&{-54}\\0&1&{-7}\\\end{array}}\right|}\right.\left.{\begin{array}{*{20}c}0\\{108}\\{15}\\\end{array}}\right)\to\left({\left.{\begin{array}{*{20}c}1&2&3\\0&0&1\\0&1&{-7}\\\end{array}}\right|}\right.\left.{\begin{array}{*{20}c}0\\{-2}\\{15}\\\end{array}}\right)$
$\left\{\begin{gathered}x=4\\y=1\\z=-2\\\end{gathered}\right.$
De oplossing van het stelsel is $(x,y,z)=(4,1,-2)$
Het Gauss-Jordan-algoritme
Bij het stelsel $\left\{\begin{gathered}x_1+3x_2+4x_3=8\\x_1+2x_2+5x_3=13\\3x_1+x_2-x_3=1\\\end{gathered}\right.$
hoort de aangevulde matrix
$\left({\left.{\begin{array}{*{20}c}1&3&4\\1&2&5\\3&1&{-1}\\\end{array}}\right|}\right.\left.{\begin{array}{*{20}c}8\\{13}\\1\\\end{array}}\right)$
Door de vegen in kolommen krijg je de matrix
$\left({\left.{\begin{array}{*{20}c}1&3&4\\0&1&{-1}\\0&0&1\\\end{array}}\right|}\right.\left.{\begin{array}{*{20}c}8\\{-5}\\3\\\end{array}}\right)$
De matrix staat nu in de rij-echelonvorm.
Matrix in rij-echelonvorm
- Elk leidend element in de matrix is gelijk aan 1
- De niet-nulrijen zijn zo geordend dat elke volgende rij met meer nullen begint
- Eventuele nulrijen staan onderaan in de matrix
De matrix $\left({\left.{\begin{array}{*{20}c}1&3&4\\0&1&{-1}\\0&0&1\\\end{array}}\right|}\right.\left.{\begin{array}{*{20}c}8\\{-5}\\3\\\end{array}}\right)$ kan worden omgevormd tot de matrix
$\left({\left.{\begin{array}{*{20}c}1&0&0\\0&1&0\\0&0&1\\\end{array}}\right|}\right.\left.{\begin{array}{*{20}c}2\\{-2}\\3\\\end{array}}\right)$
Deze matrix staat in de gereduceerde rij-echelonvorm.
Matrix in gereduceerde rij-echelonvorm
- De matrix staat in de rij-echelonvorm
- In een kolom met een leidende 1 is elk ander element gelijk aan 0
Het omvormen van een matrix in rij-echelonvorm tot een matrix in gereduceerde rij-echelonvorm gaat met het vegen in kolommen met behulp van de leidende elementen.
Dit heet het Gauss-Jordan-algoritme.
- Zie ook uitgewerkt
Elementaire rijbewerkingen
- Je mag twee rijen verwisselen
- Je mag een rij vermenigvuldigen met een getal dat niet nul is
- Je mag een veelvoud van een rij optellen bij een andere rij
Twee matrices zijn rij-equivalent als ze uit elkaar ontstaan door één of meer elementaire rij-bewerkingen.
Vegen in kolommen
In het voorbeeld is de oplossing gevonden door te vegen in kolommen. Eerst is er in de eerste kolom geveegd. Dat wil zeggen dat er in de kolom één 1 staat en verder nullen komen te staan. Er is geveegd met het element 1 in de eerste rij en eerste kolom. Het element waarmee je veegt heet het spilelement of kortweg de spil.
Het aantal oplossingen van een stelsel
- Een stelsel van $n$ lineaire vergelijkingen met $n$ variabelen kan één, geen of oneindig veel oplossingen hebben.
Voorbeeld 1
Bij het stelsel $\left\{\begin{gathered}x+2y=10\\2x-y=5\\\end{gathered}\right.$ hoort de aangevulde matrix $A=\left({\left.{\begin{array}{*{20}c}1&2\\2&{-1}\\\end{array}}\right|\begin{array}{*{20}c}{10}\\5\\\end{array}}\right)$
De matrix $A$ is om te vormen tot $\left({\left.{\begin{array}{*{20}c}1&0\\0&1\\\end{array}}\right|\begin{array}{*{20}c}4\\3\\\end{array}}\right)$
Het stelsel heeft één oplossing. De oplossing is $(x,y)=(4,3)$. Het stelsel is samenhangend en bepaald.
Voorbeeld 2
Bij het stelsel $\left\{\begin{gathered}x+2y=10\\x+2y=5\\\end{gathered}\right.$ hoort de aangevulde matrix $B=\left({\left.{\begin{array}{*{20}c}1&2\\1&2\\\end{array}}\right|\begin{array}{*{20}c}{10}\\5\\\end{array}}\right)$
De matrix $B$ is om te vormen tot $\left({\left.{\begin{array}{*{20}c}1&2\\0&0\\\end{array}}\right|\begin{array}{*{20}c}0\\5\\\end{array}}\right)$
Het stelsel heeft geen oplossing. Uit de onderste rij volgt $0x+0y=1$ en hieraan voldoet geen enkele oplossing $(x,y)$. Het stelsel is niet-samenhangend. De vergelijkingen van het stelsel zijn strijdig.
Aantal oplossingen van stelsels
Een stelsel van $n$ lineaire vergelijkingen met $n$ variabelen is:
- samenhangend en bepaald als er één oplossing is
- niet-samenhangend als er geen oplossing is
- samenhangend en onbepaald als er oneindig veel oplossingen zijn
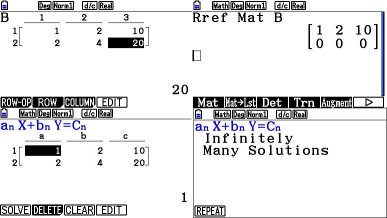
Voorbeeld 3
Bij het stelsel $\left\{\begin{gathered}x+2y=10\\2x+4y=20\\\end{gathered}\right.$ hoort de aangevulde matrix $C=\left({\left.{\begin{array}{*{20}c}1&2\\2&4\\\end{array}}\right|\begin{array}{*{20}c}{10}\\{20}\\\end{array}}\right)$
De matrix $C$ is om te vormen tot $\left({\left.{\begin{array}{*{20}c}1&2\\0&0\\\end{array}}\right|\begin{array}{*{20}c}{10}\\0\\\end{array}}\right)$
Het stelsel heeft oneindig veel oplossingen. Uit de onderste rij volgt de ware bewering $0x+0y=0$. Uit de overblijvende rij volgt $x+2y=10$ en hieraan voldoen oneindig veel oplossingen $(x,y)$. Het stelsel is samenhangend en onbepaald. De vergelijkingen van het stelsel zijn afhankelijk.