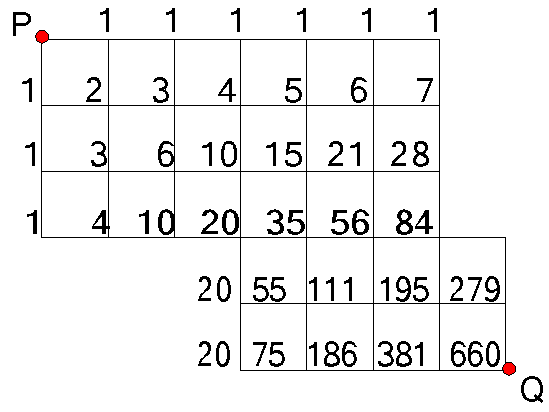4. combinaties toepassen
Werken met permutaties en combinaties
Bij de terugblik op pag. 127 staat een mooi voorbeeld.
Uit een groep van 13 jongens en 16 meisjes worden 5 leerlingen gekozen. Het aantal groepen met minstens 4 meisjes is de som van het aantal manieren waarop je '1 jongen en 4 meisjes' kan kiezen en het aantal manieren waarop je '5 meisjes kan kiezen'.
$
\left( {\begin{array}{*{20}c}
{16}\\
4\\
\end{array}}\right)\times\left({\begin{array}{*{20}c}
{13}\\
1\\
\end{array}} \right) + \left( {\begin{array}{*{20}c}
{16}\\
5\\
\end{array}} \right) = 28028
$
Uit een groep van 13 jongens en 16 meisjes wordt een comité gekozen dat bestaat uit een voorzitter, een secretaris en een penningmeester. Het aantal comités dat je kan kiezen van alleen jongens of alleen meisjes is de som van het aantal manieren met alleen jongens en het aantal manieren met alleen meisjes.
$
\left( {13} \right)_3 + \left( {16} \right)_3 = 5076
$
Rijtjes met A's en B's
Als je 10 keer met een muntstuk gooit dan zijn er $
\left( {\begin{array}{*{20}c}
{10}\\
3\\
\end{array}} \right)
$ series met 3 keer munt.

Hoeveel verschillende rijtjes kan je maken als je 3 A's en 7 B's hebt?
$
\left( {\begin{array}{*{20}c}
{10}\\
3\\
\end{array}} \right)
$
Met dobbelstenen gooien
Als je 5 keer met een dobbelsteen gooit dan zijn er 65 mogelijke uitkomsten.
Om in totaal 7 ogen te gooien kijk je naar 'vier enen en een drie' en 'drie enen en een twee'. Andere mogelijkheden zijn er niet.
$
\left( {\begin{array}{*{20}c}
5\\
4\\
\end{array}} \right) + \left( {\begin{array}{*{20}c}
5\\
3\\
\end{array}} \right) = 15
$
Het aantal mogelijkheden als je met twee enen begint is:
$1·1·6·6·6=216$
Routes in een rooster
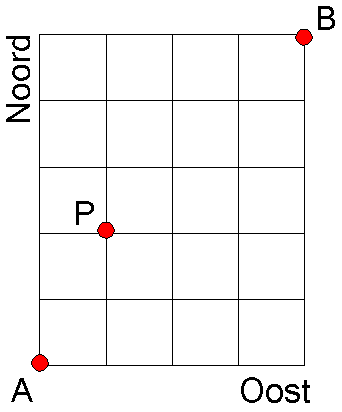
Het aantal routes van A naar B in het rooster is gelijk aan:
$
\left( {\begin{array}{*{20}c}
9\\
4\\
\end{array}} \right) = 126
$
Je moet immers 9 keer een keuze maken tussen 'Oost' en 'Noord' en daarbij 4 keer 'Oost' kiezen.
Maar $
\left( {\begin{array}{*{20}c}
9\\
5\\
\end{array}} \right)
$ kan natuurlijk ook.
Het aantal kortste routes van A naar B via P is gelijk aan:
$
\left( {\begin{array}{*{20}c}
3\\
1\\
\end{array}} \right) \times \left( {\begin{array}{*{20}c}
6\\
3\\
\end{array}} \right) = 60
$
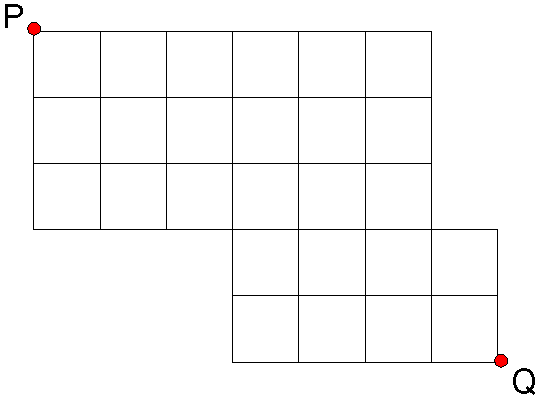
Onvolledige roosters
Om in een onvolledig rooster het aantal routes van P naar Q te bepalen zet je bij elk kruispunt het aantal routes om er vanuit P te komen.