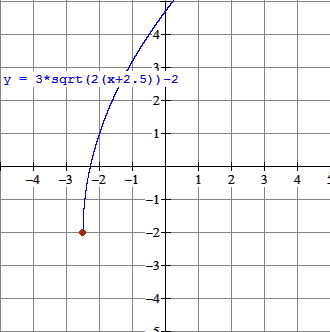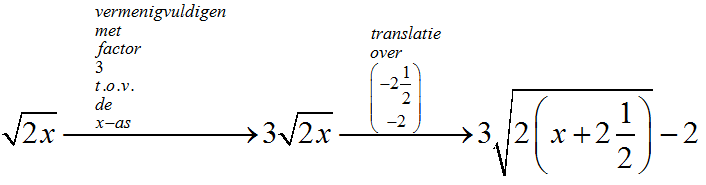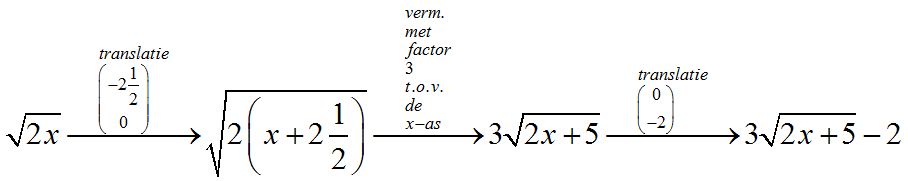Opgave 1

Teken de grafiek van:
$f(x)=3\sqrt{2x+5}-2$.

• Geef het domein en bereik
• Op welke manier kan de grafiek van $f$ worden gevonden uit de grafiek van:
  $g(x)=\sqrt{2x}$?

Uitwerking

1. Het startpunt is $(-2\frac{1}{2},-2)$
2. De grafiek gaat naar rechts
3. De grafiek gaat omhoog
4. $D_f:[-2\frac{1}{2},\to>$
5. $B_f:[-2,\to>$
6. Extra punten zijn $(-2,1)$ en $(2,7)$

Zie grafiek

Transformatie

Van $g(x)=\sqrt{2x}$ naar $f(x)=3\sqrt{2x+5}-2$:

1. Vermenigvuldigen met een factor 3 t.o.v. de $x$-as
2. Translatie over $
   \left( {\begin{array}{*{20}c}
      {-2\frac{1}{2}}  \\
      { - 2}  \\
   \end{array}} \right)
   $

De kortste route...

Alternatieve oplossing

1. Translatie over $
   \left( {\begin{array}{*{20}c}
      { - 2\frac{1}{2}}  \\
      0  \\
   \end{array}} \right)
   $
2. Vermenigvuldigen met factor 3 t.o.v. de $x$-as
3. Translatie over $
   \left( {\begin{array}{*{20}c}
      0  \\
      { - 2}  \\
   \end{array}} \right)
   $

Dat kan ook...