uitwerkingen
opgave 1
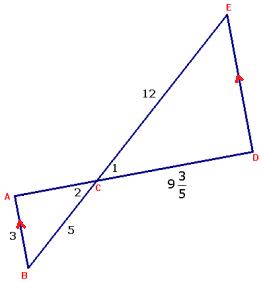
$\eqalign{& \Delta ABC \sim \Delta DEC\,\,(zandloperfiguur)\cr & \frac{{AC}}{{9\frac{3}{5}}} = \frac{5}{{12}} \Rightarrow AC = 4\cr & \angle A = 90^\circ \cr & \sin \angle C_2 = \frac{3}{5} \Rightarrow \angle C_2 \approx 37^\circ \cr & \angle E = \angle B \Rightarrow \angle E \approx 53^\circ \cr} $
opgave 2
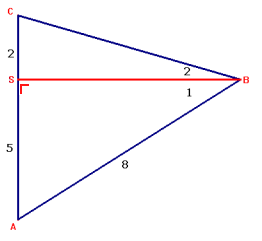
$\eqalign{& \cos \angle A = \frac{5}{8} \Rightarrow \angle A \approx 51^\circ \cr & \angle B_1 \approx 39^\circ \cr & BS = \sqrt {39} \,\,(Pythagoras) \cr & \tan \angle B_2 = \frac{2}{{\sqrt {39} }} \Rightarrow \angle B_2 \approx 18^\circ \cr & \angle B \approx 57^\circ \cr & \angle C \approx 72^\circ \,\,(som\,\,van\,\,de\,\,hoeken) \cr}$
opgave 3
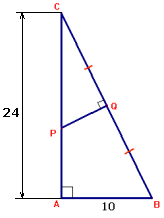
$\eqalign{& BC = 26\,\,(Pythagoras) \cr & QC=13 \cr & \Delta ABC \sim \Delta QPC \cr & \frac{{AC}}{{AB}}=\frac{{QC}}{{PQ}}\Rightarrow \frac{{24}}{{10}} = \frac{{13}}{{PQ}} \Rightarrow PQ = 5\frac{5}{{12}} \cr & \tan \angle CPQ = \frac{{13}}{{5\frac{5}{{12}}}} \Rightarrow \angle CPQ \approx 67^\circ \cr & \angle APQ \approx 113^\circ \cr & Opp(\Delta PQC) = \frac{1}{2} \cdot 13 \cdot 5\frac{5}{{12}} = 35\frac{5}{{24}} \cr} $
opgave 4
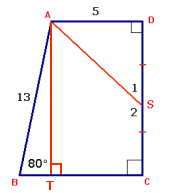
$\eqalign{& Teken\,\,een\,\,hulplijn\,\,AT \cr & \sin 80^\circ = \frac{{AT}}{{13}} \Rightarrow AT \approx 12,8 \cr & CD \approx 12,8 \Rightarrow SD \approx 6,4 \cr & \tan \angle S_1 = \frac{5}{{6,4}} \Rightarrow \angle S_1 \approx 38^\circ \cr & \angle S_2 \approx 142^\circ \cr & AC \approx 13,7\,\,(Pythagoras) \cr} $