uitwerkingen
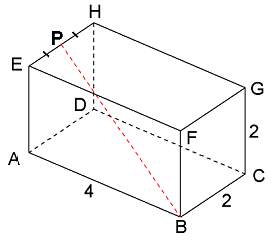
In driehoek PAB weet je al AB=4.
Bereken AP=$
\sqrt 5
$.
Met de stelling van Pythagoras vind je dan PB=$
\sqrt {21}
$
In de rechthoekig driehoek PBQ geldt:
$
\sin \angle PBQ = \frac{{PQ}}
{{PR}} = \frac{2}
{{\sqrt {21} }}$ $\Rightarrow$ $\angle PBQ \approx 26^\circ
$
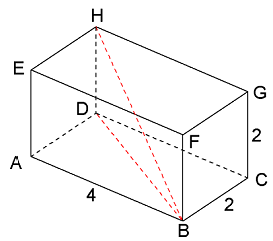
In driehoek HBD is DH=2.
Bereken DB=$
\sqrt {20}
$.
$
\tan \angle DBH = \frac{2}
{{\sqrt {20} }} \Rightarrow \angle DBH \approx 24^\circ
$
RH=$
\sqrt 5
$, HC=$
\sqrt {20}
$ en RC=$
\sqrt {21}
$, dus gaat niet lukken!
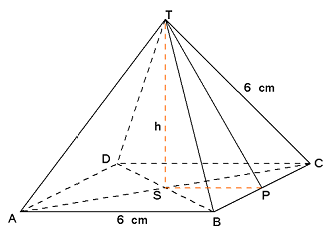
In driehoek SPT weet je SP=3.
Bereken PT=$
\sqrt {27}
$
$
\cos \angle SPT = \frac{3}
{{\sqrt {27} }} \Rightarrow \angle SPT \approx 55^\circ
$
$
\tan 55^\circ = \frac{h}
{3}$ $\Rightarrow$ $h = 4,24...\,\,cm = 42\,\,mm
$
Maar dat kon natuurlijk ook met de stelling van Pythagoras.