3. formules vergelijken
Ongelijkheden oplossen
De reparatiebedrijven I en II hanteren de volgende tarieven:
$B_I=25t+82$
$B_{II}=30t+55$
Hierin is $B$ het bedrag in euro's en $t$ de reparatietijd in uren.
- Voor welke waarden van $t$ is welk bedrijf het voordeligst?

Uitwerking
Voor welke $t$ is bedrijf I goedkoper?
Oftewel: Voor welke $t$ geldt: $25t+82<30t+55$.
Gebruik je GR:
- In het GRAPH-menu teken je de grafieken. Neem x=0..10 en y=0..400
- Met G-solve kan het snijpunt aflezen.
- Voor welke waarde van $t$ is bedrijf I goedkoper?
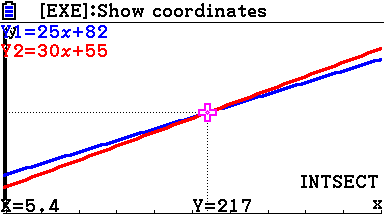
Antwoord
- Voor klussen die langer duren van 5 uur 24 minuten is bedrijf I goedkoper.
Vergelijkingen algebraisch oplossen
Algebraische oplossen betekent dat je al schrijvend stap voor stap naar de oplossing toewerkt:
- Staan er haakjes? Werk ze weg.
- Staan er breuken? Werk ze weg.
- Breng alle termen met $x$ naar het linkerlid en de rest naar het rechterlid.
- Herleid beide leden en deel door het getal dat voor $x$ staat.
Voorbeeld 1
$25x+82=15x+110$
$10x+82=110$
$10x=28$
$x=2,8$
Voorbeeld 2
$3(x+2)=9-x$$3x+6=9-x$
$4x=3$
$x=\frac{3}{4}$
Voorbeeld 3
$\frac{1}{2}x+\frac{2}{3}=\frac{3}{4}x-1$
$6x+8=9x-12$
$-3x=-20$
$x=6\frac{2}{3}$
Voorbeeld 4
$3-(a+\frac{1}{5})=2,8$
$a+\frac{1}{5}=0,2$
$a=0$
Vergelijkingen opstellen
Neem 's aan je hebt 70 munten. Dat zijn munten van 1 euro en munten van 2 euro. De totale waarde is 110 euro.
- Hoeveel munten van 1 euro heb je dan?

Uitwerking
Neem $x$ is het aantal ééneuromunten en $y$ is het aantal twee-euromunten. Dan geldt:
$x+y=70$ en $x+2y=110$
Neem nu (bijvoorbeeld) $y=70-x$ en vul dat in de tweede vergelijking in. Je krijgt dan:
$x+2(70-x)=110$
$x+140-2x=110$
$-x=-30$
$x=30$
Je hebt dan 30 ééneuromunten en 40 twee-euromunten.
Opdracht 1
Bij bedrijf A betaal je voor schoonmaakwerkzaamheden een vast bedrag van 400 euro en 21 euro per uur dat er gewerkt wordt.
Bij bedrijf B betaal je voor dezelfde werkzaamheden een vast bedrag van 100 euro, maar dan 42 euro per uur dat er gewerkt moet worden.
Neem $B$ voor het bedrag dat je betaalt en $t$ voor het aantal uren dat er gewerkt en stel vergelijkingen op.
- Voor welk aantal uren is bedrijf A duurder dan bedrijf B?
Opdracht 2
Los algebraisch op. Rond zo nodig af op één decimaal. (A44)
$
\begin{array}{l}
a.\,\,\,3x - 7 = - \frac{1}{2}x + 3\frac{1}{2} \\
b.\,\,\,x(x + 2) = x^2 + 16 \\
c.\,\,\,(x + 3)(x - 1) = x(x + 8) - 20 \\
d.\,\,\,\frac{5}{3}(3x - 4) - \frac{1}{3} = 2x + 11 \\
e.\,\,\,125 + 37,5x = 5x + 14,2 \\
f.\,\,\,(x + 2)^2 = 20 - x + x^2 \\
\end{array}
$
Opdracht 3
De queteletindex is een index die de verhouding tussen lengte en gewicht bij een persoon weergeeft. De index wordt veel gebruikt om een indicatie te krijgen of er sprake is van overgewicht of ondergewicht.
$
\eqalign{Q_{index} = \frac{m}{{h^2 }}}
$
Met m: massa in kg en h:lengte in meter.
Bij een normaal gewicht ligt de $Q_{index}$ tussen de $15$ en $20$. Joanneke is 1,73 meter lang.
- Bij welk gewicht is er bij Joanneke sprake van een normaal gewicht?
Opdracht 4
Het leger van koning Willem I bestaat uit ridders te paard en strijders te voet. Er zijn 100 man en 320 benen.
- Uit hoeveel ridders te paard bestaat dit leger?

Opdracht 1 uitwerking
Stel eerst formules op:
$B_A=400+21t$
$B_B=100+42t$
Dit geeft: $400+21t>100+42t$
Met je GR:
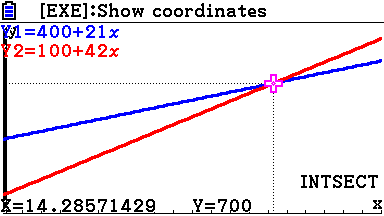
Bij klussen van 14 uur en minder is bedrijf A duurder.
Opdracht 2 uitwerking
a.
$
\begin{array}{l}
3x - 7 = - \frac{1}{2}x + 3\frac{1}{2} \\
6x - 14 = - x + 7 \\
7x = 21 \\
x = 3 \\
\end{array}
$
b.
$
\begin{array}{l}
x(x + 2) = x^2 + 16 \\
x^2 + 2x = x^2 + 16 \\
2x = 16 \\
x = 8 \\
\end{array}
$
c.
$
\begin{array}{l}
(x + 3)(x - 1) = x(x + 8) - 20 \\
x^2 + 2x - 3 = x^2 + 8x - 20 \\
2x - 3 = 8x - 20 \\
- 6x = - 17 \\
x = 2\frac{5}{6} \\
\end{array}
$
d.
$
\begin{array}{l}
\frac{5}{3}(3x - 4) - \frac{1}{3} = 2x + 11 \\
5(3x - 4) - 1 = 6x + 33 \\
15x - 20 - 1 = 6x + 33 \\
15x - 21 = 6x + 33 \\
9x = 54 \\
x = 6 \\
\end{array}
$
e.
$
\begin{array}{l}
125 + 37,5x = 5x + 14,2 \\
32,5x = 139,2 \\
x = 4,3 \\
\end{array}
$
f.
$
\begin{array}{l}
(x + 2)^2 = 20 - x + x^2 \\
x^2 + 4x + 4 = 20 - x + x^2 \\
4x + 4 = 20 - x \\
5x = 16 \\
x = 3\frac{1}{5} \\
\end{array}
$
Opdracht 3 uitwerking
Met $h=1,73$ moet gelden:
$15\lt\frac{m}{1,73^2}\lt20$
Uitwerken geeft:
$44,9\lt m \lt 59,9$

Opdracht 4 uitwerking
Neem $x$ voor de ridders te paard en $y$ voor de strijders te voet. Er zijn twee vergelijkingen:
$x+y=100$
$6x+2y=320$
Neem $y=100-x$ en vul dat in de tweede vergelijking in:
$6x+2(100-x)=320$
$6x+200-2x=320$
$4x=120$
$x=30$
Er zijn 30 ridders te paard en 70 strijders te voet.
