Weekpuzzel 8

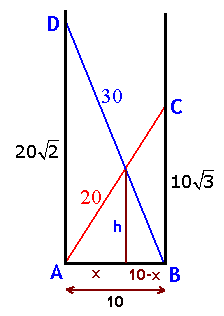
In een steeg van 10 meter breed staan twee ladders. Een ladder van 20 en een ladder van 30 meter. Zie tekening.

• Bereken exact op welke hoogte de ladders elkaar kruizen.

---

$
\eqalign{
  & AD = 20\sqrt 2 \,\,\,en\,\,\,BC = 10\sqrt 3   \cr
  & {\text{geeft:}}  \cr
  & \frac{{20\sqrt 2 }}
{{10}} = \frac{h}
{{10 - x}} \Rightarrow x = 10 - \frac{1}
{4}\sqrt 2  \cdot h  \cr
  & {\text{en}}  \cr
  & \frac{{10\sqrt 3 }}
{{10}} = \frac{h}
{x} \Rightarrow x = \frac{1}
{3}\sqrt 3  \cdot h  \cr
  & {\text{dus:}}  \cr
  & \frac{1}
{3}\sqrt 3  \cdot h = 10 - \frac{1}
{4}\sqrt 2  \cdot h  \cr
  & h = 16\sqrt 3  - 12\sqrt 2  \cr}
$

---

---

De hoogte is $16\sqrt{3}-12\sqrt{2}$

---