voorbeeldopgave
Opgave
In vaas $A$ zitten $x$ rode en $6$ gele knikkers. In vaas $B$ zitten $8$ knikkers, waarvan $x$ rode. De rest zijn gele knikkers. Rob pakt uit elke vaas 1 knikker.
- Druk de kans dat Rob uit vaas $A$ een rode knikker pakt uit in $x$.
- Toon aan dat de kans dat Rob $2$ rode knikkers pakt gelijk is aan $\eqalign{\frac{x^2}{8x+48}}$
- Bereken algebraisch het aantal rode knikkers in vaas $A$ als gegeven is dat P(Rob pakt $2$ rode knikkers) = $\eqalign{\frac{1}{5}}$
- Toon aan P(Rob pakt 2 gele knikkers) = $\eqalign{\frac{24-3x}{4x + 24}}$
Uitwerking
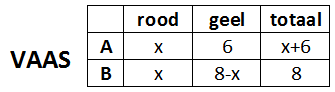
- P(rode knikker uit A)=$\eqalign{\frac{x}{x+6}}$
-
P(rode knikker uit B)=$\eqalign{\frac{x}{8}}$
P(2 rode knikkers)=$\eqalign{\frac{x}{x+6}\cdot\frac{x}{8}=\frac{x^2}{8x+48}}$ -
$
\eqalign{\frac{{x^2 }}
{{8x + 48}} = \frac{1}
{5}}
$
$
5x^2 = 8x + 48
$
$
5x^2 - 8x - 48 = 0
$
$
\eqalign{...}
$
$
x = - 2\frac{2}
{5}\,\,(v.n.)\,\,of\,\,x = 4
$
Het aantal rode knikker in vaas $A$ is gelijk aan $4$. -
P(geel uit A)=$\eqalign{\frac{6}{{x + 6}}}$
P(geel uit B)=$\eqalign{\frac{{8 - x}}{8}}$
P(2 geel)=$\eqalign{\frac{6}{{x + 6}} \cdot \frac{{8 - x}}{8} = \frac{{48 - 6x}}{{8x + 48}} = \frac{{24 - 3x}}{{4x + 24}}}$
