Transformaties van grafieken
Voorbeeld
Hoe maak je van de grafiek van $y = \sin (x)$ de grafiek van $y = - 2 + 3 \cdot \sin \left( {\frac{{2\pi }}{6}\left( {x - 2} \right)} \right)$.
Uitwerking
$y = \sin (x)$
- vermenigvuldigen met de factor $\frac{6}{{2\pi }}$ t.o.v. de $y$-as geeft:
$y = \sin \left( {\frac{{2\pi }}{6}x} \right)$
- verschuif de grafiek $2$ naar rechts:
$y = \sin \left( {\frac{{2\pi }}{6}\left( {x - 2} \right)} \right)$
- vermenigvuldig de grafiek met de factor $3$ t.o.v. de $x$-as:
$y = 3\cdot\sin \left( {\frac{{2\pi }}{6}\left( {x - 2} \right)} \right)$
- verschuif de grafiek 2 omlaag:
$y = - 2 + 3\sin \left( {\frac{{2\pi }}{6}\left( {x - 2} \right)} \right)$
Aanpak
Zoals je ziet werk je van 'binnen' naar 'buiten'. Je begint met de vermenigvuldiging t.o.v. de $y$-as. Dat is verreweg de lastigste transformatie en die heb je dan maar vast gehad.
Vermenigvuldigen met de factor p t.o.v. de y-as
- Vervang $x$ in het functievoorschrift door $\frac{1}{p}x$.
- In het functievoorschrift was $c=\frac{2\pi}{6}$ dus de factor is het omgekeerde $\frac{6}{2\pi}$.
- Je kunt ook zeggen de periode is $6$, dus $c=\frac{2\pi}{6}$
Horizontale verschuiving met p
- Vervang $x$ in het functievoorschrift door $x-p$ als je $p$ naar rechts verschuift.
- In het functievoorschrift vervang je $x$ door $x-2$ omdat je $2$ naar rechts verschuift.
Vermenigvuldigen met de factor p t.o.v. de x-as
- Vermenig het gehele functievoorschrift met de factor p.
Verticale verplaatsing met p
- Tel bij het functievoorschrift de waarde van p op.
Spiegelen in x- of y-as
Je kunt ook spiegelen in de x- en y-as. Maar dat is 'eigenlijk' hetzelfde als vermenigvuldigen met een factor $-1$ t.o.v. de $x$-as respectievelijk vermenigvuldigen met de factor $-1$ t.o.v. de $y$-as.
Gebruik de standaardvorm
Soms staat het functievoorschrift in een andere vorm dan de standaardvorm die we steeds gebruiken. Het is dan handig om het functievoorschrift in de standaardvorm te schrijven:
- $y = 4 + 5 \cdot \sin \left( {3x - 6} \right)$ wordt dan $y = 4 + 5 \cdot \sin \left( {3\left( {x - 2} \right)} \right)$.
Je kunt dan gemakkelijk de waarden van a, b, c en d bepalen.
$a=4$ dus de evenwichtsstand is $y=4$
$b=5$ dus de amplitude is $5$
$c=3$ dus de periode is $\frac{2}{3}\pi$
$d=2$ dus de verticale verplaatsing is $2$ naar rechts
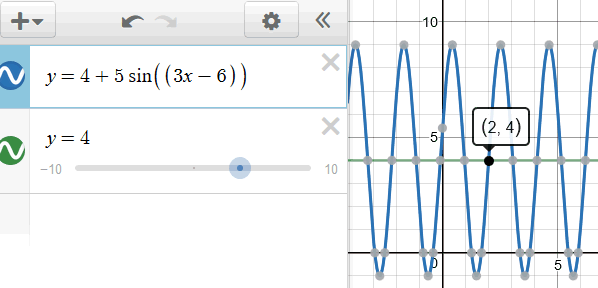
Opdracht 1
Geef aan hoe de grafiek van $f(x)=2-3\cdot\sin(3(x-1))$ uit de standaardgrafiek van $y=\sin(x)$ onstaat en geef de evenwichtsstand, de amplitude, de periode en de coördinaten van het beginpunt.
Opdracht 2
De grafiek van $g$ ontstaat uit die van $y=\sin(x)$ door eerst te vermenigvuldigen ten opzichte van de $y$-as met $\pi$, de grafiek $\pi$ naar links te verschuifen, daarna te vermenigvuldigen met de factor $\pi$ ten opzichte van de $x$-as en vervolgens de grafiek $\pi$ naar boven te verschuiven.
- Stel een functievoorschrift van $g$ op.