De hoogte van de toren
Korte beschrijving
- Onderwerp: Leerlingen meten de hoogte van een boom en van een toren.
- Voorkennis: Gelijkvormige driehoeken, rekenen met verhoudingen en formules. Vergelijkingen oplossen.
- Materiaal: Meetlint, vlak spiegeltje en een stok van 1 meter.
- Plaats: Buiten meten, binnen berekenen.
- Uitgevoerd: In HAVO 3. [december 1995]
In dit blokuur willen we de hoogte van de Refter gaan meten of om precies te zijn: hoe hoog is het hoogste puntje van de toren van de Refter ten opzichte van de plaats waar de school staat?
Voordat we daar mee gaan beginnen doen we eerst wat oefeningen en behandelen we wat theorie over hoogtemeting.
De hoogte van de vlaggenmast.
Voor de school staan twee vlaggenmasten. Zonder in de mast te klimmen kun je met behulp van een spiegeltje en een meetlint de hoogte van een van deze vlaggenmasten meten.
De methode gaat als volgt:
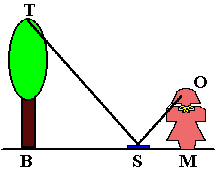
Hiernaast zie je hoe je de hoogte van de boom in B kan meten. Je legt op een ‘willekeurig’ afstand een spiegeltje (S) neer. Je gaat dan zover van het spiegeltje staan dat je in het midden van het spiegeltje precies de top van de boom ziet. Je meet vervolgens de afstand BS, SM en OM. (OM is de afstand van de grond tot je oog)
Het is belangrijk dat je goed recht staat en dat het spiegeltje goed horizontaal ligt.
Omdat je hier te maken hebt met twee gelijkvormige driehoeken kan je de hoogte van de boom uitrekenen.
- Ga naar buiten en gebruik deze methode om de hoogte van de vlaggenmast voor de school te bepalen. Gebruik daarbij werkblad 1.
De hoogte van een toren.
De methode die je gebruikt hebt om de hoogte van de vlaggenmast te bepalen is niet geschikt om de hoogte van de Refter te bepalen. Dit komt doordat je de horizontale afstand van school tot de Refter niet kent.In een boek uit 1614 van Sybrandt staat een methode beschreven hoe je met een stok, een spiegeltje en een meetlint toch de hoogte van een toren zou kunnen bepalen.
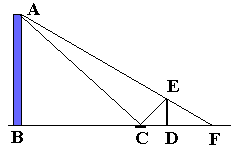
Je legt ‘ergens’ een spiegeltje neer (C). Je zet de stok DE zo neer dat je als je vanaf de bovenkant van de stok in het spiegeltje kijkt je precies in het midden van het spiegeltje de torenspits ziet. Vervolgens zoek je punt F op en wel zo dat als je vanuit F kijkt, je precies de torenspits en de bovenkant van de stok op een lijn ziet.
Je meet vervolgens CD, DE en DF. Omdat je hier te maken hebt met 3 gelijkvormige driehoeken kun je met die gegevens de hoogte van de toren AB bepalen.
Vandaag voeren we deze meting niet uit. Vooral het bepalen van punt F is lastig. Je moet echt met je hoofd op de grond gaan liggen en daar beginnen we niet aan!
- Beantwoord de vragen op werkblad 2.
Een andere methode.
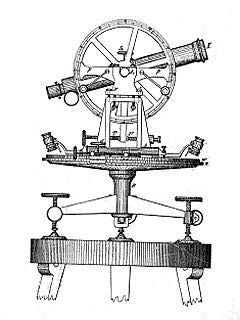Met een zogenaamde theodoliet kun je hoeken en verhoudingen bepalen van objecten op afstand. Hiernaast zie je daar een afbeelding van staan.
Het instrument dat jullie gaan gebruiken is een kleine variant op de theodoliet. Het bestaat uit twee plankjes en een latje. Op het onderste plankje en het latje zijn schaalverdelingen aangebracht. Op het onderste plankje zit ook een waterpas.
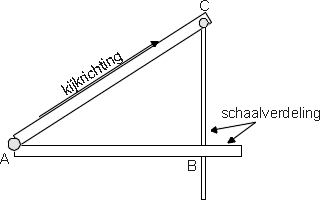
Het werkt als volgt: je zorgt dat het plankje AB goed horizontaal staat. Je zorgt er dan voor dat als je langs AC kijkt je precies de torenspits ziet. Op het latje BC zit ook een schaalverdeling, dit latje blijft altijd precies verticaal. Als je AC schuiner zet verandert dus zowel de afstand AB als de afstand BC. Het gaat om de verhouding van AB en BC.
Hieronder staat een voorbeeld:
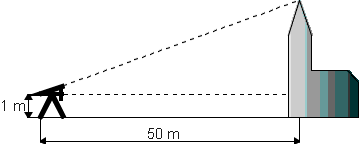
Als je de afstand van de theodoliet tot het kerkje kent en je weet de afstanden op de schaalverdeling AB en BC van de theodoliet, dan kun je de hoogte van het kerkje uitrekenen.
Het probleem is echter dat je de afstand van school tot de Refter niet kent. Wat we wel weten is dat de torenspits van de Refter 19,75 meter is, gemeten van de nok van het dak tot de bovenkant van het kruis. Met deze kennis moet je de hoogte van het hoogste puntje van de Refter t.o.v. school kunnen bepalen.
- Ga naar buiten en voer de opdrachten op werkblad 3 uit.
Inleveren
- Iedereen levert alleen de werkbladen in. Zet je naam erop en controleer of je alles hebt ingevuld.