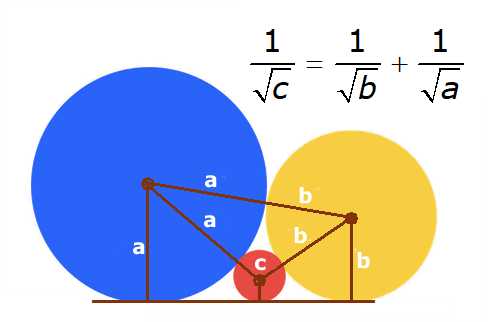
Het gevangen muisje
$
\begin{array}{l}
\left\{ \begin{array}{l}
(a - c)^2 + x^2 = (a + c)^2 \\
(b - c)^2 + y^2 = (b + c)^2 \\
(a - b)^2 + (x + y)^2 = (a + b)^2
\end{array} \right. \\
\left\{ \begin{array}{l}
a^2 - 2ac + c^2 + x^2 = a^2 + 2ac + c^2 \\
b^2 - 2bc + c^2 + y^2 = b^2 + 2bc + c^2 \\
a^2 - 2ab + b^2 + (x + y)^2 = a^2 + 2ab + b^2
\end{array} \right. \\
\left\{ \begin{array}{l}
- 2ac + x^2 = 2ac \\
- 2bc + y^2 = 2bc \\
- 2ab + (x + y)^2 = 2ab
\end{array} \right. \\
\left\{ \begin{array}{l}
x^2 = 4ac \\
y^2 = 4bc \\
(x + y)^2 = 4ab
\end{array} \right. \\
\left\{ \begin{array}{l}
x = 2\sqrt {ac} \\
y = 2\sqrt {bc} \\
x + y = 2\sqrt {ab}
\end{array} \right. \\
\end{array}
$
Dus:
$
\begin{array}{l}
2\sqrt {ab} = 2\sqrt {ac} + 2\sqrt {bc} \\
\Large\frac{{\sqrt {ab} }}{{\sqrt {abc} }} = \frac{{\sqrt {ac} }}{{\sqrt {abc} }} + \frac{{\sqrt {bc} }}{{\sqrt {abc} }} \\
\Large\frac{1}{{\sqrt c }} = \frac{1}{{\sqrt b }} + \frac{1}{{\sqrt a }} \\
\end{array}
$