ik wil een bewijs
Je moet natuurlijk nooit zo maar geloven wat iemand zegt. Hoe kun je nu weten dat die stelling van Pythagoras echt altijd klopt? Als je zeker wilt zijn dan moet er misschien wel een bewijs voor te vinden zijn... Nou, die bewijzen zijn er.
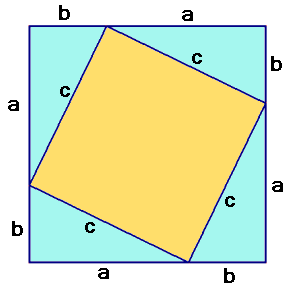
De oppervlakte van het grote vierkant is gelijk aan de oppervlakte van 4 stukken van $ Je kunt de oppervlakte van het grote vierkant ook schrijven als (a+b)2.
Dus moet gelden: (a + b)2 = 2ab + c2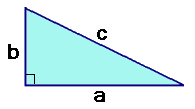 Op de schuine zijde van een willekeurige rechthoekige driehoek teken je een vierkant met zijde c. Je vult de figuur aan met dezelfde driehoeken zodat je groot vierkant krijgt.
Op de schuine zijde van een willekeurige rechthoekige driehoek teken je een vierkant met zijde c. Je vult de figuur aan met dezelfde driehoeken zodat je groot vierkant krijgt.
\frac{1}
{2}
$·a·b=2ab en het grote vierkant c2.
a2 + 2ab + b2 = c2 + 2ab
a2 + b2 = c2 ... en dat is de stelling van Pythagoras.