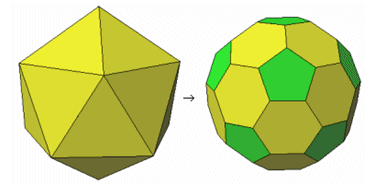
Regelmatige veelvlakken
Regelmatige veelvlakken of Platonische lichamen is een bijzondere groep van lichamen. De grensvlakken bestaan uit allemaal dezelfde regelmatige veelhoeken. Hieronder zie de vijf regelmatige veelvlakken:
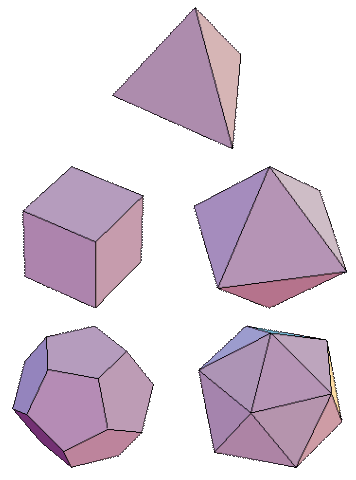
Zoals je ziet zijn er maar drie verschillende grensvlakken: een gelijkzijdige driehoek, een vierkant en een regelmatige vijfhoek.
Opdracht 1
Print de bouwplaten platonische lichamen uit en zet ze in elkaar.
Opdracht 2
Vul onderstaande tabel in:
|
Naam |
Aantal ribben |
Aantal grens-vlakken |
Aantal hoek-punten |
|
Tetraëder |
6 |
... |
... |
|
Kubus |
12 |
... |
... |
|
Octaëder |
... |
... |
... |
|
Dodecaëder |
... |
... |
... |
|
Ikosaëder |
... |
... |
... |
Wat valt je op?
Opdracht 3
Je ziet hier een stukje uit een Engels boek:“For any polyhedron topologically equivalent to a sphere – in particular convex polyhedron – the Euler formula holds: v + f = 2 + e, where v is the number of vertices, e is the number of edges, and f is the number of faces.”
Er is hier sprake van een formule. Wat wordt er met de formule bedoeld? Controleer of de formule klopt voor de lichamen in de tabel van opgave 2.
Opdracht 4
Waarom kun je van regelmatige zeshoeken geen lichaam maken ? En waarom lukt het met regelmatige achthoeken niet ? (Aanwijzing: kijk eens naar de verschillende grootte van de hoeken….)Opdracht 5
Hieronder staat een ander veelvlak.
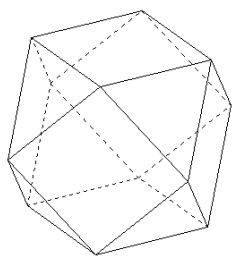
Dit is geen regelmatig veelvlak. Toch is het wel bijzonder: de grensvlakken zijn regelmatige veelhoeken, maar ze zijn alleen niet allemaal hetzelfde.
- Wat is de naam van dit lichaam?
- Lichamen met regelmatige veelhoeken zal zijvlakken noemen we halfregelmatige veelvlakken. Welke andere naam wordt ook gebruikt?
- Klopt de formule van opdracht 3 hier ook?
| Eindopdracht |
Blijkbaar is het mogelijk om door afknotting van een regelmatig veelvlak een halfregelmatig veelvlak te krijgen. Althans in 7 van de 13 gevallen.
|