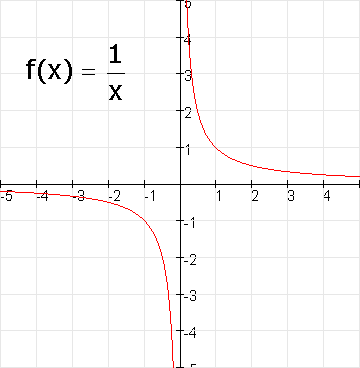Wat is een asymptoot?
Neem de functie y=$\eqalign{\frac{1}{x}}$. Je begint met $x=1$ en bereken $f(x)$. Neem dan de helft van $x$ en bereken $f(x)$, enz... Je komt dan steeds dichter bij de $y$-as, maar je komt er nooit. $f(x)$ wordt steeds maar groter en groter...
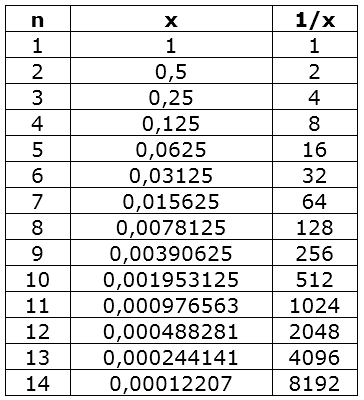
De lijn $x=0$ (de y-as) noemen we een asymptoot.
Je kunt ook met $x=-1$ starten en 't hetzelfde doen. Ook dan kom je steeds dichter bij de lijn $x=0$ maar je komt er nooit. Nu wordt $f(x)$ steeds kleiner en kleiner...
Je kunt ook bij $x=1$ beginnen en dan steeds verdubbelen... $x=2$, $x=4$, $x=8$, ... $f(x)$ wordt dan steeds kleiner en kleiner... Maar dan is dan een ander soort 'kleiner' dan net.
Idem voor starten bij $x=-1$ en dan steeds verdubbelen...