Je gooit met een munt en een dobbelsteen. Wat is de kans dat je 'kop' of 'vijf ogen' gooit?

Iemand geeft als antwoord:

De kans op kop is een $\frac{1}{2}$, de kans op vijf is $\frac{1}{6}$. Het is een OF-kans, dus de kans op een kop of vijf is gelijk aan $\frac{1}{2}+\frac{1}{6}=\frac{2}{3}$. Denk maar aan de somregel.

• Welke 'denkfout' maakt deze persoon?

Dat klopt niet. De voorwaarde voor het gebruik van de somregel was dat de gebeurtenissen elkaar moesten uitsluiten. Dat is hier niet het geval. Je kunt best kop gooien en ook vijf ogen.

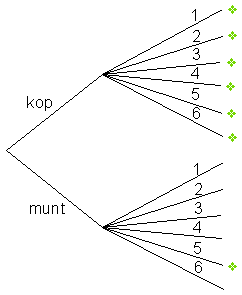
In de kansboom hiernaast kan je zien dat 7 takken van de 12 voldoen. De kans op 'kop' of 'vijf ogen' is $\frac{7}{12}$.

Wiskundig gezien kan je dat ook zo formuleren:

$P(A\,of\,B)=P(A)+P(B)-P(A\,en\,B)$

$P(kop\,of\,5\,ogen)=\frac{1}{2}+\frac{1}{6}-\frac{1}{12}=\frac{7}{12}$

---