2. Breuken
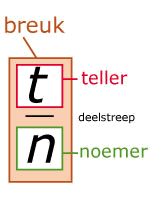
Als je breuken wilt vereenvoudigen kan je teller en noemer door hetzelfde getal delen.
Gelijknamig maken
Je kan ook teller en noemer vermenigvuldigen met hetzelfde getal. Dat gebruik je als je breuken gelijknamig wilt maken.
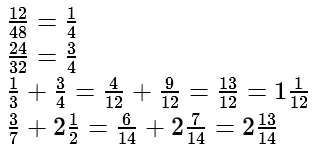
Wat voor het rekenen met getallen geldt geldt ook voor het rekenen met variabelen. Je kunt teller en noemer vermenigvuldigen of delen met hetzelfde getal of variabele.
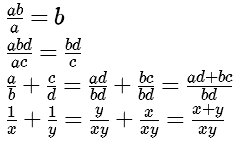
Vermenigvuldigen van breuken
Als je breuken wilt vermenigvuldigen dan vermenigvuldig je teller met de teller en noemer met de noemer.
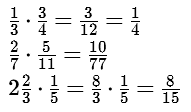
Hezelfde doe je als je rekent met breuken waarin variabelen voorkomen.
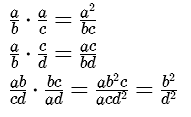
Zoals je ziet kan je door teller en noemer te delen door dezelfde variabele breuken met variabelen vereenvoudigen.
Het delen van breuken
Er zijn twee manieren waarop je breuken kunt delen. De eerste methode is gelijknamig maken en de tweede methode is gebruik maken van de regel 'delen door een breuk is vermenigvuldigen met het omgekeerde'.
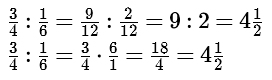
Hetzelfde kan je doen bij het delen van breuken waarin variabelen voorkomen.
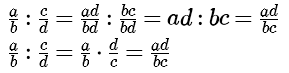
Voorbeelden van herleiden
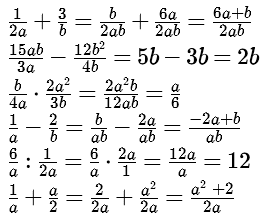
Soms kan je breuken eerst vereenvoudigen voordat je ze op gaat tellen of vermenigvuldigen. Let goed op het verschil tussen optellen en vermenigvuldigen.
Opdracht 2
Herleid onderstaande formules. Dat wil zeggen: schrijf de formules zo kort mogelijk.
$
\eqalign{
& a.\,\,\,\frac{{3a^3 b^2 }}
{{2ab^2 }} = \cr
& b.\,\,\,\frac{b}
{{4a}} \cdot \frac{{2a^2 }}
{{3b}} = \cr
& c.\,\,\,\frac{{3a^7 \cdot 6a^6 }}
{{9a^4 }} = \cr
& d.\,\,\,\frac{{2a}}
{{4ab}} \cdot \frac{{6ab}}
{3} = \cr
& e.\,\,\,\frac{{15ab}}
{{3a}} - \frac{{12b^2 }}
{{4b}} = \cr
& f.\,\,\,\frac{{9a^2 b^3 c^4 }}
{{3abc}} = \cr
& g.\,\,\,\frac{{a + 1}}
{a} - \frac{1}
{a} = \cr
& h.\,\,\,x + \frac{{xy}}
{y} + \frac{{xy^2 }}
{{y^2 }} = \cr}
$