4. Machten
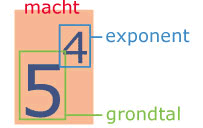
Een macht is herhaald vermenigvuldigen.
- $5^{4}=5\cdot5\cdot5\cdot5$
Een belangrijke regel is dat als je twee machten met hezelfde grondtal vermenigvuldigt dan kan je de exponenten optellen.
- $p^4 \cdot p^5 = p^{4+5} = p^9$
Als je de macht van een macht uitrekent dan vermenigvuldig je de exponenten.
- $\left( {p^3 } \right)^4 = p^{3 \times 4} = p^{12}$
Machten en negatieve getallen
Er is een groot verschil tussen $-3^{2}$ en $(-3)^{2}$:
- $-3^{2}$ is het getal $3$ in het kwadraat met een min ervoor. Dat is dan $-9$.
- $(-3)^{2}$ is het getal $-3$ in het kwadraat en dat is $9$.
Als je $(-2)^{3}$ uitrekent dan komt daar $-8$ uit en als je $(-2)^{4}$ uitrekent dan komt daar $16$ uit. Als je de macht van een negatief getal uitrekent dan hangt het 'teken' af of de exponent 'even' of 'oneven' is.
-
$
\left({ - 2} \right)^3=-8
$ -
$
\left({-2}\right)^4=16
$ -
$
\left({-2} \right)^5=-32
$ - ...
Je kunt ook de macht van producten uitrekenen.
-
$
\left({-2ab}\right)^2=4a^2b^2
$ -
$
\left({3a^2b}\right)^3=27a^6b^3
$ -
$
\left({-ab^2c^3}\right)^5=-a^5b^{10}c^{15}
$
Herleiden
Daarmee kun je al heel veel uitdrukkingen herleiden. Hieronder zie je daar een aantal voorbeelden van. Controleer de antwoorden en ga na welke regels je daarvoor gebruikt:
$a^6\cdot a^5+a^4=a^{11}+a^4$
$-(-3x^2)^3\cdot2y^4=54x^6y^4$
$\left({-2x}\right)^3\cdot\left({2y}\right)^3-\left({xy}\right)^3=-65x^3y^3$
$\Large\frac{{\left({-p^2q}\right)^3}}{{-p^3q^2}}$=$p^3q$
Opdracht 4
Herleid onderstaande formules. Dat wil zeggen: schrijf de formules zonder haakjes en zo kort mogelijk.
$
\eqalign{
& a.\,\,\,\,2p^6 \cdot 3p^8 = \cr
& b.\,\,\,\,7x^2 \cdot ( - x)^7 = \cr
& c.\,\,\,\,\left( { - 3a} \right)^2 \cdot \left( { - 2a} \right)^3 = \cr
& d.\,\,\,\,\left( {3a^2 b^3 } \right)^2 = \cr
& e.\,\,\,\,\left( { - abc} \right)^4 \cdot \left( {abc} \right)^4 = \cr
& f.\,\,\,\left( {3x^2 y^4 \cdot 2xy^5 } \right)^2 = \cr
& g.\,\,\,\,\frac{{\left( {2p} \right)^2 }}
{{p^2 }} = \cr
& h.\,\,\,\,\frac{{4a^2 b}}
{{\left( {2ab} \right)^2 }} = \cr
& i.\,\,\,\,\frac{{\left( { - pq^2 } \right)^3 }}
{{\left( {pq} \right){}^2}} = \cr}
$