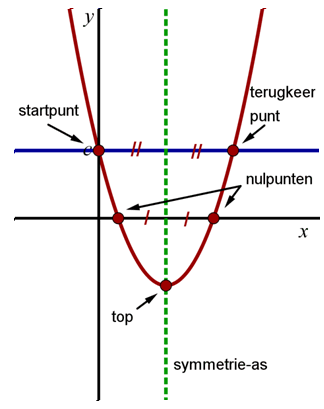
de algemene vorm
Een kwadratische formule heeft als algemene vorm: $y=ax^{2}+bx+c$.
De grafiek bij deze formule is een parabool.
-
Getal $a$ (ook wel afbuigingsfactor genoemd) bepaalt de 'wijdte' van de grafiek.
$a>0$: dalparabool
$a<0$: bergparabool -
Het snijpunt met de $y$-as heet het startpunt.
Dat is het punt $(0,c)$ -
Het andere punt met $y=x$ het het terugkeerpunt.
Los op: $ax^{2}+bx+c=c$ en je krijgt $x=-\frac{b}{a}$ -
De top ligt precies in het midden tussen start en terugkeerpunt.
$x{}_{top}$ is het midden van $x=0$ en $x=-\frac{b}{a}$
$x{}_{top}$=$-\frac{b}{2a}$ -
De snijpunten met de $x-as$ heten nulpunten.
Los op $ax^{2}+bx+c=0$ -
De symmetrie-as is de verticale lijn door de top.
$x=x{}_{top}$