Een voorbeeld uit de 4e klas HAVO wiskunde B
Gegeven een kegel. De diameter van het grondvlak is 12 en de hoogte is 8. In de kegel past precies een bol.
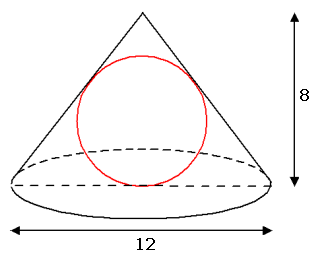
Je wilt dan de straal van de bol weten. Maak een tekening:
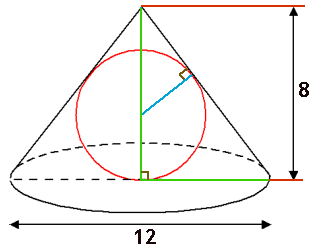
De straal is $r$. Je krijgt dan:
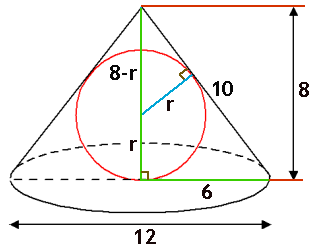
...en daar herken je dan misschien een snavelfiguur in...!? Maar dan anders...:-)
Gelijkvormigheid
Als je dat netjes doet zoals in de derde klas dan kan het bijna niet fout gaan:
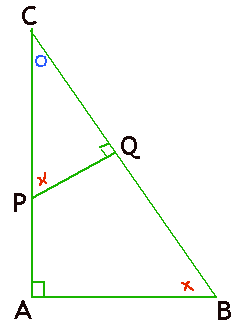
Driehoek ABC is gelijkvormig met driehoek PQC, maar dan moet je nog wel even precies opschrijven hoe dat zit. Dus bepaal de overeenkomstige hoeken.
$\Delta$ABC~$\Delta$...
$\angle$A is gelijk aan $\angle$Q, want die zijn beide 90$^o$.
$\angle$C is gelijk aan $\angle$C (triviaal:-)
$\angle$B is gelijk aan $\angle$P, want de som van de hoeken is 180$^o$
$\Delta$ABC~$\Delta$QPC
Als je dit hebt dan het je het intelligente werk gedaan. Nu is het nog slechts een kwestie van 'tekstverwerken', dus tabel maken, opschrijven wat je weet... en hopen dat je voldoende gegevens hebt om $r$ uit te rekenen. Dat gaat dan zo:
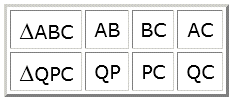
Invullen:
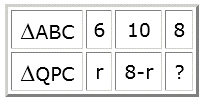
Kruislings vermenigvuldigen geeft:
$\begin{array}{l} 6(8 - r) = 10 \cdot r \\ 48 - 6r = 10r \\ 16r = 48 \\ r = 3 \\ \end{array} $