3. cirkelvergelijkingen

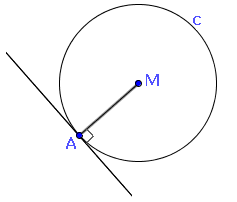
De cirkelvergelijking (x-a)2+(y-b)2=r2 De cirkel met middelpunt $M(a,b)$ en straal $r$ heeft als vergelijking: $(x-a)^2+(y-b)^2=r^2$ Omdat een raaklijn van een cirkel loodrecht staat op de straal naar het raakpunt, is de straal van de cirkel gelijk aan de afstand van $M$ tot $k$, dus $r=d(M,k)$ Voorbeeld Stel een vergelijking op van de cirkel $c$ met middelpunt $M(3,4)$ die de lijn $k:y=\frac{1}{2}x$ raakt. Aanpak Stel een vergelijking op voor de lijn $l$ die door M gaat en loodrecht staat op $k$. Bereken het snijpunt $A$ van $l$ en $k$. $r=d(M,k)=d(M,A)$ De vergelijking wordt $c:(x-3)^2+(y-4)^2=r^2$    De uitwerking staat in je boek op bladzijde 108.

Kwadraatafsplitsen Voor het herleiden van de vergelijking $x^2+y^2-4x+6y-3=0$ tot de vorm $(x-2)^2+(y+3)^2=16$ gebruik je de techniek van het kwadraatafsplitsen. Voorbeeld Wat is het middelpunt en de straal van de cirkel met vergelijking $x^2+y^2+8x-2y+6=0$? Uitwerking $x^2+y^2+8x-2y+6=0$ $x^2+8x+y^2-2y+6=0$ $(x+4)^2-16+(y-1)^2-1+6=0$ $(x+4)^2+(y-1)^2-11=0$ $(x+4)^2+(y-1)^2=11$ Het middelpunt is $M(-4,1)$ en de straal is $r=\sqrt{11}$ Kwadraatafsplitsen Kwadraatafsplitsen is een tweedegraads formule schrijven als een kwadraat. 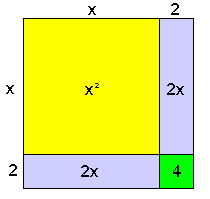Op kwadraatafsplitsen staat uitleg... Je kunt HIER oefenen.... filmpje!

De cirkelvergelijking x2+y2+ax+by+c=0 Door de vergelijking $x^2+y^2+6x-8y+15=0$ te schrijven in de vorm $(x-a)^2+(y-b)^2=r^2$ kun je zien dat je met een cirkel met middelpunt $(a,b)$ en straal $r$ te maken hebt. Je gebruikt daarbij kwadraatafsplitsen. De afstand van een punt tot een kromme is de lengte van het korste verbindingslijnstuk tussen het punt en de kromme. 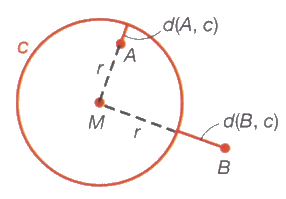Afstand van punt tot cirkel $c$ met middelpunt $M$ en straal $r$ Voor punt $A$ binnen $c$ geldt $d(A,c)=r-d(M,A)$ Voor punt $B$ buiten $c$ geldt $d(B,c)=d(M,B)-r$

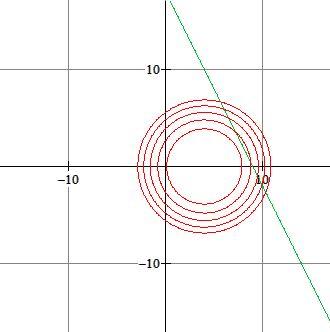
Denkactiviteit Bereken voor welke waarde van $a$ de lijn $k:2x+y=18$ raakt aan de cirkel $c:x^2+y^2-8x+a=0$ Antwoord $a=-4$ Zie uitwerking

bladzijde 108
kan dat ook met een bol?
kwadraatafsplitsen
uitwerking