|
Vectoren
Een vector heeft een lengte en een richting. Je geeft vectoren aan met kentallen.
$
\overrightarrow {OA} = \left( {\begin{array}{*{20}c}
{-1}\\
2\\
\end{array}} \right)
$ of $
\underline a = \left( {\begin{array}{*{20}c}
3\\
{-2}\\
\end{array}} \right)
$
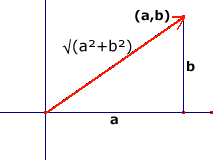
De lengte van $\underline a$ is:
$
\left| {\underline a } \right| = \sqrt {3^2 + \left( { - 2} \right)^2 } = \sqrt {13}
$
|
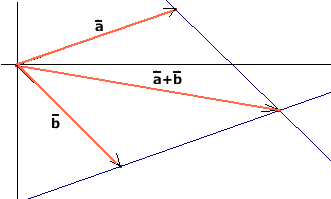
Optellen
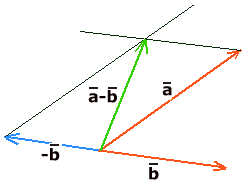
Aftrekken
|
|
Vermenigvuldigen met een getal

Met $
\underline a = \left( {\begin{array}{*{20}c}
2\\
1\\
\end{array}} \right)
$ en $
\underline b = \left( {\begin{array}{*{20}c}
{-1}\\
{-3}\\
\end{array}} \right)
$:
$
2\underline a - 3\underline b = 2\left( {\begin{array}{*{20}c}
2\\
1\\
\end{array}} \right) - 3\left( {\begin{array}{*{20}c}
{-1}\\
{-3}\\
\end{array}} \right) = \left( {\begin{array}{*{20}c}
7\\
{11}\\
\end{array}} \right)
$
|
Vectorvoorstelling van een lijn
$
k:\left( {\begin{array}{*{20}c}
x\\
y\\
\end{array}} \right) = \left( {\begin{array}{*{20}c}
{-1}\\
2\\
\end{array}} \right) + \lambda \left( {\begin{array}{*{20}c}
3\\
1\\
\end{array}} \right)
$
$
\left( {\begin{array}{*{20}c}
{-1}\\
2\\
\end{array}} \right)
$ is de steunvector
$
\left( {\begin{array}{*{20}c}
3\\
1\\
\end{array}} \right)
$ is de richtingsvector.
Voorbeeld
De lijn $k$ gaat door de punten $A(-1,2)$ en $B(3,1)$.
-
Stel een vectorvoorstelling op van de lijn k.
Zie uitwerking
|










