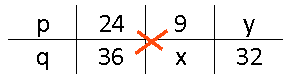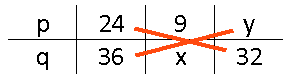|
Kruisproducten
In een verhoudingstabel gelden allerlei wetmatigheden. Een handige manier om 'onbekenden' uit te rekenen is met gebruik te maken van kruislings vermenigvuldigen.
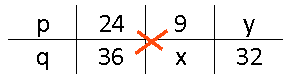 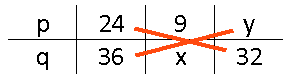
|
Rechthoekige driehoeken
Een rechthoekige driehoek heeft een rechte hoek, twee rechthoekszijden en een schuine zijde.
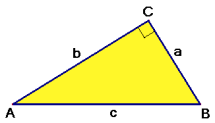
De rechthoekszijde $BC$ ligt tegenover $\angle A$. Daarom heet de zijde $BC$ de overstaande rechthoekszijde van $\angle A$.
De rechthoekszijde $AC$ is een been van $\angle A$. Zijde $AC$ heet de aanliggende rechthoekszijde van $\angle A$.
|
|
De tangens
De tangens is een voorbeeld van een goniometrische verhouding.
Dat wil zeggen dat de waarde van de tangens de verhouding geeft van de twee rechthoekszijden van een rechthoekige driehoek.
Omdat de tangens een verhouding aangeeft kan je bij berekeningen gebruik maken van een verhoudingstabel.


|
Voorbeeld
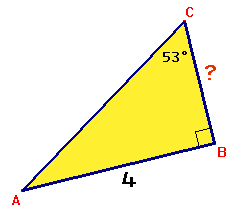
$\angle C=53^o$ en $AB=4$. In een verhoudingtabel wordt dat:

Met kruislings vermenigvuldigen kan je waarde van $BC$ berekenen.
$tan(53^o)\times BC=1\times4$
$\eqalign{BC=\frac{4}{tan(53^o)}\approx3}$
|