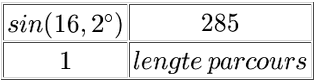|
De tangens
Een helling met hellingshoek $A$ met een hellingsgetal van 0,3. Dat is een hellingspercentage van 30%.
Het hellingsgetal heet de tangens van $\angle A$.
-
$\tan(\angle A)=0,3$
-
Met je rekenmachine: $\angle A\approx 16,7^\circ$
$\eqalign{\tan(\angle A)=\frac{overstaande\,rhz\,van\,\angle A}{aanliggende\,rhz\,van \angle A}}$
Zie berekeningen met tangens voor de verschillende berekeningen in een rechthoekige driehoek.
|
De sinus en de cosinus
Bij een helling is de sinus van de hellingshoek gelijk aan de verticale verplaatsing gedeeld door de lengte van het parcours.
Bij een helling is de cosinus van de hellingshoek gelijk aan de horizontale verplaatsing gedeeld door de lengte van het parcours.
Meer in 't algemeen:
$\eqalign{\sin(\angle A)=\frac{overstaande\,rhz\,van\,\angle A}{schuine\,zijde}}$
$\eqalign{\cos(\angle A)=\frac{aanliggende\,rhz\,van\,\angle A}{schuine\,zijde}}$
|
|
Voorbeeld
Van een skihelling is de hoogte 285 meter en de hellingshoek is 16,2$^\circ$.
-
Bereken de lengte van het parcours in meters, Rond af op één decimaal.

|
Uitwerking
$\eqalign{sin(\angle A)=\frac{verticaal}{lengte\,parcours}}$
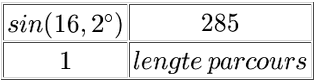
$lengte\,parcours=\eqalign{\frac{1·285}{sin(16,2^\circ)}\approx1021,5\,m}$
|