|
Ruimtefiguren en uitslagen
Ruimtefiguren worden ook wel lichamen genoemd. Voorbeelden zijn prisma's, piramides,...
Een prisma is een lichaam dat begrensd wordt door twee evenwijdige zijvlakken. De overige zijvlakken zijn rechthoeken.
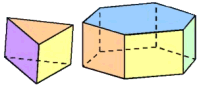
Een piramide is een lichaam waarvan alle hoekpunten op één na in één vlak liggen. Dat ene hoekpunt heet de top. De andere hoekpunten liggen in het grondvlak.
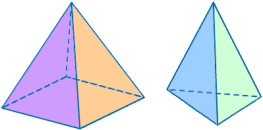
Er is van alles mogelijk: een driezijdige piramide (ook wel viervlak genoemd), een vijfzijdige piramide, een regelmatige vierzijdige primaide, enz.
Bij een regelmatige n-zijdige piramide is het grondvlak een regelmatige veelhoek en zijn de opstaande ribben allemaal even lang.
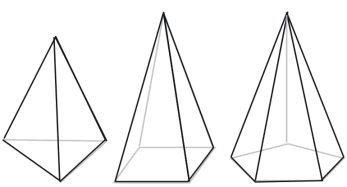
Uitslag van een piramide
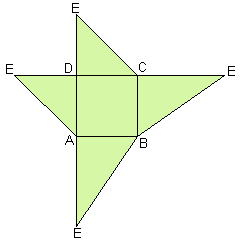
Je ziet hier de uitslag van een piramide. Deze piramide heeft het vierkant ABCD als grondvlak en punt E bevindt zich recht boven het punt D waarbij DE=CD.
|
Uitslagen van een cilinder
Van een ruimtefiguur kan je een uitslag maken. Er zijn verschillende utslagen mogelijk.
Een uitslag van een lichaam is een vlakke figuur die je krijgt als je het lichaam openknipt.
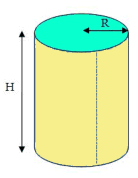 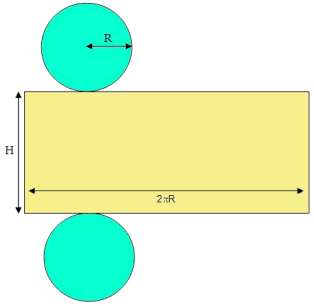
De omtrek van een cirkel met straal $r$ is $2\pi·r$
Een touwtje spannen
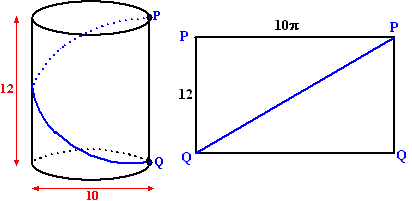
Opgave
Hierboven zie je hoe een touwtje gespannen is over de cilindermantel van een cilinder. Bereken op 1 decimaal nauwkeurig de lengte van het touwtje als
-
het touwtje 1 keer rond gaat
-
het touwtje 2 keer rond gaat
Zie er wordt een touwtje gespannen
|
|
Uitslagen van kegels
Een kegel bestaat uit een grondcirkel een een gebogen vlak: de kegelmantel.
De uitslag van een kegel bestaat uit een cirkelsector en een cirkel (de grondcirkel). De lengte van de boog van de cirkelsector moet precies gelijk zijn aan de omtrek van de grondcirkel.
De middelpuntshoek in het voorbeeld hierboven is $180^\circ$. Met de straal van de cirkelsector en de middelpuntshoek kun je de lengte van de boog van de cirkelsector uitrekenen en andersom...:-)
De straal van de grondcirkel geven we aan met $r$ en de straal van de cirkelsector (de kegelmantel) met $R$.
|
Voorbeeld
Van een kegel is gegeven dat $r=3$ en $R=5$.
-
Bereken de middelpuntshoek van de uitslag van deze kegel.
Aanpak
Gebruik dat de lengte van de cirkelboog in de cirkelsector gelijk is aan de omtrek van de grondcirkel.
Uitgewerkt
Ik kies $\alpha$ als de middelpuntshoek. De omtrek van de grondcirkel ($r=3$) is gelijk aan $2\pi·3=6\pi$. De boog van de cirkelsector voor de kegelmantel is dan ook $6\pi$ lang en omdat $R=5$ moet gelden:
$\eqalign{\frac{\alpha}{360^\circ}·10\pi=6\pi}$
$\alpha=216^\circ$
|














