|
Oppervlakte van cilinders
De oppervlakte van een cilinder is gelijk aan de oppervlakte van de uitslag van de cilinder... d.w.z. twee maal de oppervlakte van de (grond-)cirkel en de oppervlakte van de cilindermantel.
$O_{cilinder}=2·\pi r^2+2\pi r·h$
Voorbeeld
Bereken exact de oppervlakte van een cilinder met $r=3$ en $h=4$.
Uitwerking
$O_{cilinder}=2·\pi·3^2+2·\pi·3·4=18\pi+24\pi=42\pi$
|
Oppervlakte van kegels
De oppervlakte van een kegelmantel is $\pi rR$. Hierin is $r$ de straal van de grondcirkel en $R$ de straal van de uitslag van de kegelmantel.
$O_{kegel}=\pi r^2+\pi rR$
Voorbeeld
Bereken exact de oppervlakte van een kegel met $r=3$ en $h=4$.
Uitwerking
Bereken $R$ met de stelling van Pythagoras. $R=5$.
$O_{kegel}=\pi·3^2+\pi·3·5=9\pi+15\pi=24\pi$
|
|
Oppervlakte van bollen
De oppervlakte van een bol is $4\pi r^2$. Hierin is $r$ de straal van de bol.
$O_{bol}=4\pi r^2$
Voorbeeld
Bereken exact de oppervlakte van een bol met straal 3.
Uitwerking
$O_{bol}=4·\pi·3^2=36\pi$
|
Formules
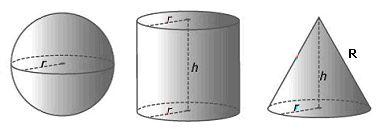
$O_{bol}=4\pi r^2$
$O_{cilinder}=2·\pi r^2+2\pi r·h$
$O_{kegel}=\pi r^2+\pi rR$
|
|
Opgave 1
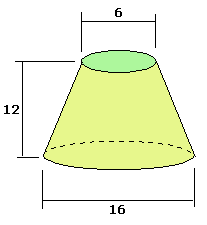
Je ziet hier een afgeknotte kegel, met d1=6, d2=16 en h=12.
-
Bereken de oppervlakte van deze afgeknotte kegel op 1 decimaal nauwkeurig.
|
Opgave 2
Van een kegel is de oppervlakte van de grondcirkel 30 cm² en de oppervlakte van de kegelmantel 75 cm².
-
Bereken de tophoek van de kegel.
Opgave 3
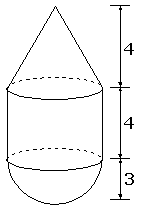
Dit object bestaat uit een kegel, cilinder en een halve bol.
-
Bereken de oppervlakte op 1 decimaal nauwkeurig.
|









