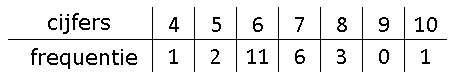|
Klassenindeling en frequentiepolygoon
frequentietabel
In een frequentietabel kun je aflezen hoe vaak een waarnemingsgetal voorkomt. Dit kan een absolute frequentie zijn (zie onder) maar ook een relatieve frequentie.
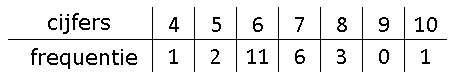
histogram
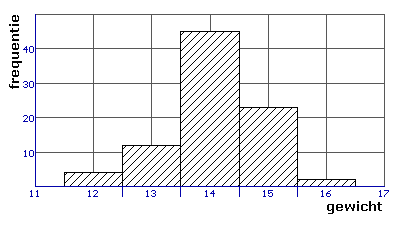
Bij een histogram heb je kwantitatieve gegevens op de horizontale as. De staven liggen tegen elkaar.
Een histogram is een bijzonder geval van een staafdiagram.
frequentiepolygoon
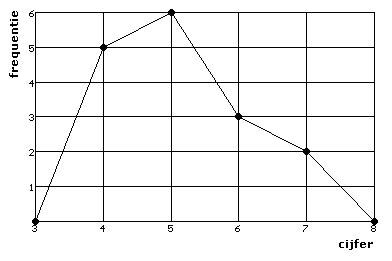
De frequentiepolygoon is een lijndiagram waarin boven elk waarnemingsgetal de frequentie is uitgezet. Begin en eindpunt liggen op de horizontale as.
Je kunt ook de relatieve frequenties gebruiken. Je spreekt dan van een relatieve frequentiepolygoon.
klassenindeling
Om een beetje handig met grote aantallen gegevens om te kunnen gaan brengen we ze meestal onder in klassen.
Zo'n klassenindeling varieert meestal van 5 tot 10 klassen met gelijke klassenbreedte.
boxplot
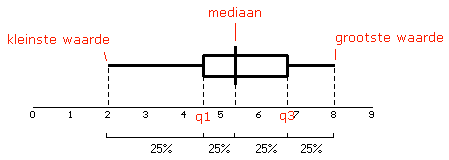
|
Cumumatieve-frequentiepolygoon
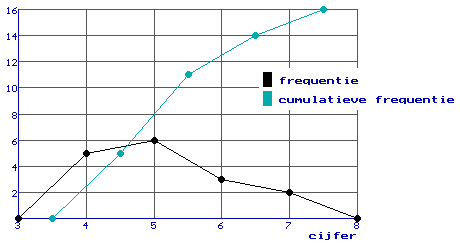
Bij een somfrequentiepolygoon gebruik je de cumulatieve frequenties. Je zet ze daarbij boven de rechterklassengrens uit.
Voorbeeld 1
Gegeven is een tabel met cijfers en bijbehorende frequenties:

We willen een cumulatieve frequentiepolygoon tekenen met relatieve frequenties. We maken eerst een kolom met cumulatieve frequenties en daarna een kolom met de relatieve cumulatieve frequenties.

Je kunt nu met de cijfers en de relatieve cumulatieve frequenties een frequentiepolygoon tekenen. Gebruik daarbij de rechter klassengrenzen!
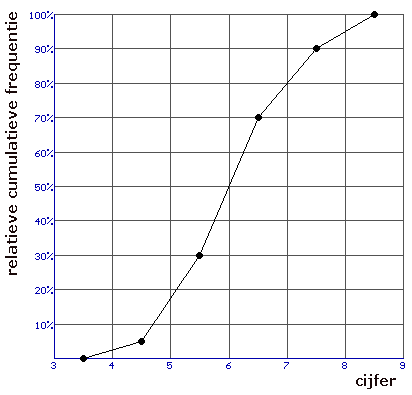
|
|
Centrummaten
Met centrum-maten geef je het 'midden' van een verdeling aan. Bij veel verdelingen liggen de getallen 'rond' een bepaald getal. Met een centrummaat geef je aan waar de getallen zo'n beetje om heen liggen.
Om het gemiddelde van een aantal getallen te berekenen tel je alle getallen op en deel je de som door het aantal.
De mediaan is het midden van een verdeling, dat wil zeggen dat 50% van de getallen onder de mediaan ligt en 50% erboven.
Je kunt ook zeggen: de mediaan is het middelste getal als je de getallen op volgorde van klein naar groot zet. Bij een oneven aantal getallen kan dat, maar bij een even aantal is het lastiger. In dat geval nemen we als mediaan het rekenkundig gemiddelde van de twee middelste getallen.
De modus van een serie getallen is het getal met de hoogste frequentie. Het getal wat het meeste voorkomt.
|
Voorbeeld 2
Gegeven de volgende klassenindeling:

-
bereken de 3 centrummaten
Zie uitwerking
|