|
Bouten en moeren
Van een partij bouten is de diameter $X$ normaal verdeeld met $\mu_X=13,2$ mm en $\sigma_X=0,1$ mm en van een partij moeren is de diameter $Y$ normaal verdeeld met $\mu_Y=13,5$ mm en $\sigma_Y=0,2$ mm.
-
Welk percentage van de bouten zal te dik zijn voor een moer als telkens aselect een bout en een moer gepakt worden?
-
Met welke gemiddelde diameter moeten de moeren worden vervaardigd opdat slechts 3% van de bouten te dik zal zijn voor de moeren?
|
Uitwerking
Neem een nieuwe kansvariabele $V=Y-X$ (de diameter van de moer min de diameter van de bout ). Als $V$>0 dan past de bout in de moer.
$\mu_V=\mu_Y-\mu_X=13,5-13,2=0,3$
$\sigma_V=\sqrt{\sigma_X^2+\sigma_Y^2}=\frac{\sqrt{5}}{10}$
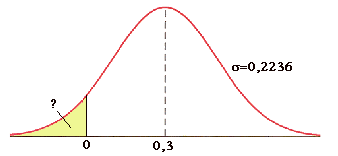
Via het startmenu van je GR:
-
NormCD(-1099,0,$\frac{\sqrt{5}}{10}$,0.3)$\to$0,089856...
Ongeveer 9,0% van bouten zal te dik zijn.
Deel 2
Je moet nu op zoek naar $x$ zodat:
-
NormCD(-1099,0,$\frac{\sqrt{5}}{10}$,$x$)$\to$0,03
Met de SOLVER (Lower=0 en Upper=20) geeft de GR:
Neem voor de moeren $\mu_Y=13,2+0,5=13,7$ mm
|







