|
De top van de parabool y=a(x-p)2+q
De top van de parabool $y=a(x-p)^2+q$ is het punt $(p,q)$.
Voorbeeld
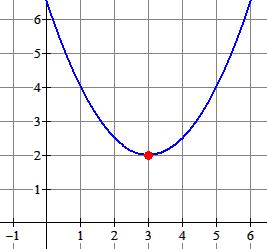
Gegeven: $f(x)=\frac{1}{2}(x-3)^2+2$.
-
De top is het punt $(3,2)$.
|
Hoe zit dat?
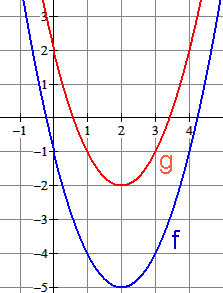
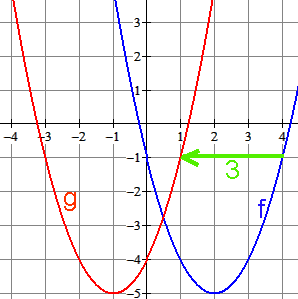
De parabool $f(x)=\frac{1}{2}x^2$ heeft als top $(0,0)$. Als je de grafiek 3 naar rechts verschuift en 2 omhoog dan verander je het functievoorschrift van $f$ zo:
-
Vervang $x$ door $x-3$
-
Tel er 2 bij op
Je krijgt $f(x)=\frac{1}{2}(x-3)^2+2$.
Voorbeelden
Geef van coördinaten van de top van:
-
$y=2(x-4)^{2}+4$
-
$y=-(x+3)^{2}-11$
-
$y=-\frac{2}{3}(x+1\frac{1}{2})^{2}+2\frac{3}{4}$
-
$y=x^{2}+3$
-
$y=(x+7)^{2}$
Zie antwoorden
|
|
Formule y=a(x-p)²+q opstellen
Als je van de parabool de coördinaten van de top kent en je weet nog een punt dan kan je met $y=a(x-p)^2+q$ een formule opstellen.
Voorbeeld
De parabool $p$ heeft als top $(3,7)$ en gaat door $(0,3)$.
-
Stel een formule op voor $p$.
|
Uitgewerkt
Je krijgt $p:y=a(x-3)^2+7$.
Vul $(0,3)$ in om $a$ te berekenen:
$a(0-3)^2+7=3$
$a·9=-4$
$a=-\frac{4}{9}$
De formule $p:y=-\frac{4}{9}(x-3)^2+7$
|