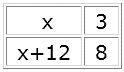|
Opgave 1
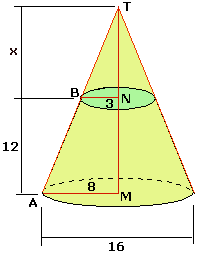
Eerst maar 's een tekening maken van de hele kegel.
$
\Delta AMT \sim \Delta BNT
$
Er geldt:
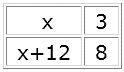
$8x=3(x+12)$
$8x=3x+36$
$5x=36$
$x=7\frac{1}{5}$
Kleine kegel
$R=7\frac{4}{5}$
$
O_{kegelmantel} = \pi \cdot 3 \cdot 7\frac{4}
{5} = 23\frac{2}
{5}\pi
$
Grote kegel
$R=20\frac{4}{5}$
$
O_{kegelmantel} = \pi \cdot 8 \cdot 20\frac{4}
{5} = 166\frac{2}
{5}\pi
$
Conclusie
$
O_{afgeknotte\,\,kegelmantel}$ = $166\frac{2}
{5}\pi - 23\frac{2}
{5}\pi = 143\pi
$
Grond- en bovenvlak
Dat zijn cirkels met r=8 resp. r=3
$
\eqalign{
& O_{grondvlak} = \pi \cdot 8^2 = 64\pi \cr
& O_{bovenvlak} = \pi \cdot 3^2 = 9\pi \cr}
$
Eindconclusie
$
\eqalign{
& O_{afgeknotte\,\,kegel}=143\pi+64\pi+9\pi=216\pi\cr
& O_{afgeknotte\,\,kegel}\approx 678,6\cr}
$
|
Opgave 2
Van een kegel is de oppervlakte van de grondcirkel 30 cm2 en de oppervlakte van de kegelmantel 75 cm2.
-
Bereken de tophoek van de kegel.
Uitwerking
Voor de halve tophoek $\alpha$ geldt:
$
\eqalign{
& \sin \alpha = \frac{r}
{R} = \frac{r}
{R} \cdot \frac{{\pi r}}
{{\pi r}} = \frac{{\pi r^2 }}
{{\pi rR}} = \frac{{30}}
{{75}} = \frac{2}
{5} \cr
& \alpha \approx 23,58^\circ \cr}
$
De tophoek is ongeveer $47,2^\circ$
Opgave 3
Vanwege de halve bol weet je dat $r=3$.
Wat heb je nodig?
-
Oppervlakte kegelmantel met $r=3$ en $R=5$
-
Cilindermantel met $r=3$ en $h=4$
-
Halve bol met $r=3$
$O_{totaal}=\pi rR+2\pi r·h+\frac{1}{2}·4\pi r^2$
$O_{totaal}=\pi·3·5+2\pi·3·4+\frac{1}{2}·4\pi·3^2$
$O_{totaal}=15\pi+24\pi+18\pi$
$O_{totaal}=57\pi$
$O_{totaal}\approx179,1$
|