|
Voorbeeld 1
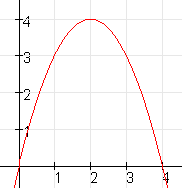
$f(x)=-x^2+4x$
-
Geef de vergelijking van de raaklijn aan f in het punt $A(1,3)$
-
De lijn $k$ raakt $f$ in $O(0,0)$ en de lijn $m$ raakt $f$ in $C(4,0)$. Bereken de coördinaten van het snijpunt van $k$ en $m$.
-
De lijn $n:y=4x+b$ raakt de grafiek van $f$. Bereken b.
Bepaal de afgeleide:
$f'(x)=-2x+4$
a.
Bereken $f'(1)=2$. De raaklijn wordt $y=2x+b$. Vul $A(1,3)$ in en je vindt $b=1$.
$y=2x+1$
b.
Bepaal de vergelijkingen van de raaklijnen door $O(0,0)$ en $C(4,0)$.
$k: y=4x$ en $m: y=-4x+16$
Om het snijpunt van $k$ en $m$ uit te rekenen los je de vergelijking $4x=-4x+16$ op:
$x=2$
$y=8$
Het snijpunt is $(2,8)$
c.
$f'(x)=4$
$-2x+4=4$
$-2x=0$
$x=0$
De raaklijn is: $y=4x$, zodat $b=0$.
|
|
 Voorbeeld 2
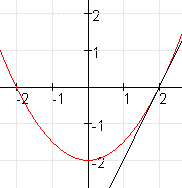
$g(x)=\frac{1}{2}x^2-2$
-
Wat is de vergelijking van de raaklijn aan $g$ die loodrecht staat op de raaklijn door het punt $D(2,0)$?
Bepaal de afgeleide:
$g'(x) = x$
$g'(2)=2$
De lijn loodrecht op de raaklijn in (2,0) heeft als richtingscoëfficiënt $-\frac{1}{2}$.
Voor welke $x$ geldt dat $g'(x)=-\frac{1}{2}$?
$g'(-\frac{1}{2})=-\frac{1}{2}$, immers $g'(x)=x$.
$g(-\frac{1}{2})=-1\frac{7}{8}$
Invullen van $(-\frac{1}{2},-1\frac{7}{8})$ in $y=-\frac{1}{2}x+b$ geeft $b=-2\frac{1}{8}$
De vergelijking is: $y=-\frac{1}{2}x-2\frac{1}{8}$
|
