|
Opgave 3
Gegeven $f(x)=x^4-50x^2+544$, bepaal de extreme waarden van f.
Bepaal $f'$:
$f'(x)=4x^3-100x$
Los de vergelijking $f'(x)=0$ op:
$
\eqalign{
& 4x^3-100x=0\cr
& 4x\left({x^2-25}\right)=0\cr
& 4x=0\vee x^2-25=0\cr
& x=0\vee x^2=25\cr
& x=0\vee x=-5\vee x=5\cr}
$
Maak een schets:
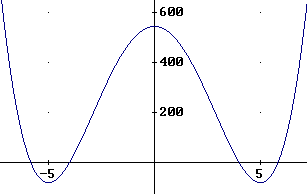
-
Het minimum bij $x=-5$ is $-81$.
-
Het maximum bij $x=0$ is $544$.
-
Het minimum bij $x=5$ is $-81$.
NOOT: het maximum is een lokaal maximum.
|
Opgave 4
Gegeven $g(x)=x^4-4x^3$, bepaal de extreme waarden van g.
Bepaal $g'(x)$:
$g'(x)=4x^3-12x^2$
Los de vergelijking $g'(x)=0$ op:
$
\eqalign{
&4x^3-12x^2=0\cr
&4x^2\left({x-3}\right)=0\cr
&4x^2=0\vee x-3=0\cr
&x=0\vee x=3\cr}
$
Maak een schets:
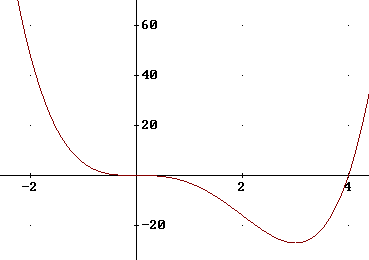
-
Het minimum bij $x=3$ is $g(3)=-27$.
Bij $x=0$ is iets anders aan de hand. Dat heet buigpunt.
|








