|
Opdracht
-
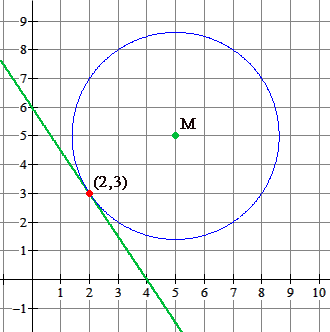
Bereken exact de afstand van het punt $M(5,5)$ tot de lijn $k:3x+2y=12$.
Tekening
-
Die $\sqrt{13}$ is precies de straal van de kleinste cirkel die je kan trekken met middelpunt $M(5,5)$ en die precies raakt aan de lijn $k:3x+2y=12$.
|
Uitwerking
Stel een formule op voor de afstand tussen het punt en de lijn uitgedrukt in $x$. Bepaal met behulp van de afgeleide de minimale afstand. Dat lijkt lastig vanweg de wortel, maar meestal valt dat mee. De wortel speelt bij het bepalen van het minimum geen rol...
-
$n:y=-1\frac{1}{2}x+6$
-
$d(A,n)=\sqrt{(x-5)^2+(-1\frac{1}{2}x+6-5)^2}$
-
$d(A,n)=\sqrt{(x-5)^2+(-1\frac{1}{2}x+1)^2}$
-
$d(A,n)=\sqrt{3\frac{1}{4}x^2-13x+26}$
$d(A,n)$ is minimaal als $3\frac{1}{4}x^2-13x+26$ minimaal is. Dus de afgeleide. De afgeleide is $6\frac{1}{2}x-13$. De afgeleide is nul bij $x=2$. Dat is inderdaad een mimimum. Je krijgt:
-
$d(A,n)=\sqrt{3\frac{1}{4}·2^2-13·2+26}=\sqrt{13}$
Ik vind het een mooie oplossing...
|







