|
Hat vaasmodel
In een vaas zitten 5 rode, 4 groene en 1 blauwe knikker. Je pakt 3 knikkers uit de vaas zonder terugleggen.
-
Bereken de kans op 3 verschillende kleuren.
Antwoord
$P(X=3)=\frac{{\left( {\begin{array}{*{20}c}
5\\
1\\
\end{array}} \right)\left( {\begin{array}{*{20}c}
4\\
1\\
\end{array}} \right)\left( {\begin{array}{*{20}c}
1\\
1\\
\end{array}} \right)}}{{\left( {\begin{array}{*{20}c}
{10}\\
3\\
\end{array}} \right)}} = \frac{1}{6}
$
Somregel
In een vaas zitten 5 rode, 4 groene en 1 blauwe knikker. Je pakt 3 knikkers uit de vaas zonder terugleggen.
-
Bereken de kans op minstens 2 rode knikkers.
$P(X\ge2)=P(X=2)+P(X=3)$
$
P(X \ge 2) = \frac{{\left( {\begin{array}{*{20}c}
5\\
2\\
\end{array}} \right)\left( {\begin{array}{*{20}c}
5\\
1\\
\end{array}} \right)}}{{\left( {\begin{array}{*{20}c}
{10}\\
3\\
\end{array}} \right)}} + \frac{{\left( {\begin{array}{*{20}c}
5\\
3\\
\end{array}} \right)}}{{\left( {\begin{array}{*{20}c}
{10}\\
3\\
\end{array}} \right)}} = \frac{1}{2}
$
Complementregel
In een vaas zitten 5 rode, 4 groene en 1 blauwe knikker. Je pakt 3 knikkers uit de vaas zonder terugleggen.
-
Bereken de kans op minstens 2 dezelfde kleur knikkers.
P(minstens 2 dezelfde kleur)=1-P(3 verschillende kleuren)
P(minstens 2 dezelfde kleur)=1-$\frac{1}{6}$
P(minstens 2 dezelfde kleur)=$\frac{5}{6}$
|
De productregel
Twee gebeurtenissen $A$ en $B$ zijn onafhankelijk als:
$P(A\cap B)=P(A)\cdot P(B)$
Voorbeeld
Je gooit met een munt en een dobbelsteen.
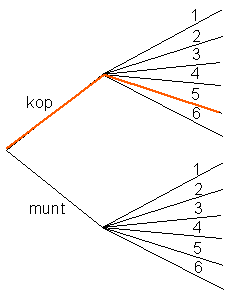
Gebeurtenis $A$: je gooit met de munt kop
Gebeurtenis $B$: je gooit 5 ogen met de dobbelsteen
De gebeurtenissen $A$ en $B$ zijn onafhankelijk.
|







