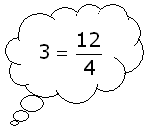-
Gegeven is
$\eqalign{\frac{{4A}}{{3\left({2t-20}\right)}}=16}$.
Druk $A$ uit in $t$.
-
Gegeven is de formule
$2P-8=0,4\sqrt{Q}$.
Druk $Q$ uit in $P$.
-
Gegeven is de formule
$\eqalign{N =\frac{{5x}}{{3y-2}}}$.
Neem $N=6$ en herleid de formule tot de vorm $x=ay+b$.
-
Maak $q$ vrij bij de formule
$\eqalign{K=5+\frac{8}{q}}$
-
Maak $B$ vrij bij de formule
$\eqalign{A=\frac{{B+4}}{{3B-2}}}$.
-
Maak $N$ vrij bij de formule
$\eqalign{3\left({1-M}\right)=2-\frac{1}{N}}$.
TIP
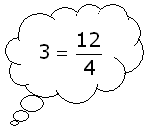
In de uitwerkingen hiernaast komt twee keer een omzetting voor van breuk naar breuk:
$\eqalign{A = \frac{B}{C} \Rightarrow C = \frac{B}{A}}$
Je kunt de $A$ en de $C$ verwisselen?
Dat is niet zo gek als je denkt aan
$\eqalign{3=\frac{12}{4}}$.
Daarbij kan je immers ook de 3 en 4 verwisselen. Is dat logisch?
Ja...als 12 gedeeld door 3 gelijk aan 4 is dan moet 12 gedeeld door 4 wel gelijk aan 3 zijn...
|
-
$\eqalign{\frac{{4A}}{{3(2t - 20)}} = 16}$
$\eqalign{
& 4A = 16 \cdot 3(2t - 20) \cr
& 4A = 48(2t - 20) \cr
& A = 12(2t - 20) \cr
& A = 24t - 240 \cr} $
-
$2P - 8 = 0,4\sqrt Q $
$\eqalign{
& 20P - 80 = 4\sqrt Q \cr
& 5p - 20 = \sqrt Q \cr
& Q = {\left( {5p - 20} \right)^2} \cr} $
-
$\eqalign{6 = \frac{{5x}}{{3y - 2}}}$
$\eqalign{
& 5x = 6\left( {3y - 2} \right) \cr
& 5x = 18y - 12 \cr
& x = 3\frac{3}{5}y - 2\frac{2}{5} \cr} $
-
$\eqalign{K = 5 + \frac{8}{q}}$
$\eqalign{
& K - 5 = \frac{8}{q} \cr
& q = \frac{8}{{K - 5}} \cr} $
-
$\eqalign{A = \frac{{B + 4}}{{3B - 2}}}$
$\eqalign{
& A(3B - 2) = B + 4 \cr
& 3AB - 2A = B + 4 \cr
& 3AB - B = 2A + 4 \cr
& B(3A - 1) = 2A + 4 \cr
& B = \frac{{2A + 4}}{{3A - 1}} \cr} $
-
$\eqalign{3\left( {1 - M} \right) = 2 - \frac{1}{N}}$
$\eqalign{
& 3 - 3M = 2 - \frac{1}{N} \cr
& \frac{1}{N} = 3M - 1 \cr
& N = \frac{1}{{3M - 1}} \cr} $
|