Antwoorden

---

De eenheidscirkel

---

Vraag 1

1. 30$^o$ immers $\frac{1}{6}\pi$ is $\frac{1}{6}$ van 180$^o$=30$^o$
2. $\frac{5}{6}\pi$, $2\frac{1}{6}\pi$ of $2\frac{5}{6}\pi$, maar ook $-1\frac{1}{6}\pi$ of $-1\frac{1}{6}\pi$, enz.
3. De sinus van $8\frac{5}{6}\pi$ is gelijk aan $\frac{1}{2}$. Het is immers modulo $2\pi$.
4. $\cos(1\frac{3}{4}\pi)=\frac{1}{2}$ en $\cos(-\frac{1}{4}\pi)=\frac{1}{2}$. Deze hoeken zijn niet gelijk aan elkaar.
5. Dat is onzin. Er zijn oneindig veel hoeken met dezelfde waarde van de sinus.

Vraag 2

1. $\sin(\frac{2}{3}\pi)=\frac{1}{2}\sqrt{3}$ en $\cos(\frac{2}{3}\pi)=-\frac{1}{2}$.
2. Dat is $\frac{1}{4}\pi$.
3. Dat is geen toeval...
   
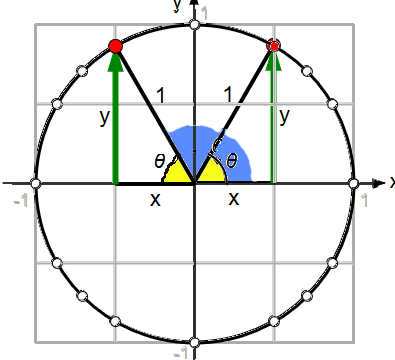
   Als de gele hoek gelijk is aan $a$ dan is de blauwe hoek gelijk aan $\pi-a$ en dat is samen gelijk aan $\pi$.
4. Je weet dan dat $\alpha+\beta=\pi+k\cdot2\pi$ met $k=\{..., -2, -1, 0, 1, 2, ....\}$
5. Je weet dan dat $\alpha+\beta=k\cdot2\pi$ met $k=\{..., -2, -1, 0, 1, 2, ....\}$

Vraag 3

1. $\sin \left( \alpha  \right) = \frac{1}{2}\sqrt 3  \Rightarrow \alpha  = \frac{1}{3}\pi  + k \cdot 2\pi  \vee \alpha  = \frac{2}{3}\pi  + k \cdot 2\pi $. Er zijn twee oneindige verzamelingen van oplossingen.
2. Zie a.
3. $\cos \left( \beta  \right) = \frac{1}{2}\sqrt 3  \Rightarrow \beta  = \frac{1}{6}\pi  + k \cdot 2\pi  \vee \beta  =  - \frac{1}{6}\pi  + k \cdot 2\pi $

Vraag 4

1. $\cos \left( \alpha  \right) = \frac{1}{2} \Rightarrow \alpha  = \frac{1}{3}\pi  + k \cdot 2\pi  \vee \alpha  =  - \frac{1}{3}\pi  + k \cdot 2\pi $
2. $\sin \left( \alpha  \right) =  - \frac{1}{2}\sqrt 2  \Rightarrow \alpha  = 1\frac{1}{4}\pi  + k \cdot 2\pi  \vee \alpha  = 1\frac{3}{4}\pi  + k \cdot 2\pi $
3. $\sin \left( \alpha  \right) = 0 \Rightarrow \alpha  = k \cdot \pi $
4. $\cos \left( \alpha  \right) = 1 \Rightarrow \alpha  = k \cdot 2\pi $
5. $\sin \left( \alpha  \right) =  - 1 \Rightarrow \alpha  = 1\frac{1}{2}\pi  + k \cdot 2\pi $
6. $\sin \left( \alpha  \right) = \cos \left( {2\frac{1}{2}\pi } \right) \Rightarrow \sin \left( \alpha  \right) = 0 \Rightarrow \alpha  = k \cdot \pi $

Grafieken van goniometrische functies

---

1. de evenwichtsstand=2, de amplitude=3, de periode=3 en de verticale verschuiving is 2
2. er geldt $d=\frac{1}{2}$, je moet kijken naar $-\sin(...)$ en die 'start' in het punt $(\frac{1}{2},2)$
3. $g(x)=3+2\cdot\sin(\frac{2\pi}{6}(x+1))$
4. $y=-1-3\cdot\sin(\frac{3\pi}{7}(x+2)$

Karakteristieke eigenschappen

---

Vraag 2

1. $y=1+2\cdot\sin(\frac{2\pi}{5}(x-3))$
2. $y=1-2\cdot\sin(\frac{2\pi}{5}(x-\frac{1}{2}))$
3. $y=1+2\cdot\cos(\frac{2\pi}{5}(x-4\frac{1}{4}))$

Transformaties van grafieken

---

Opdracht 1

$y = \sin (x)$

• Vermenigvuldigen met $\frac{1}{3}$ t.o.v. de $y$-as:

$y = \sin (3x)$

• verschuif de grafiek 1 naar rechts:

$y = \sin (3(x - 1))$

• vermenigvuldig met $-3$ t.o.v. de $x$-as:

$y =  - 3 \cdot \sin (3(x - 1))$

• verschuif de grafiek 2 omhoog:

$y = 2 - 3 \cdot \sin (3(x - 1))$

De evenwichtsstand is: y=2, de amplitude is 3 (niet -3), de periode is $\frac{2\pi}{3}$ en de coördinaten van het beginpunt zijn (1,2)

Opdracht 2

$\eqalign{y = \pi  + \pi  \cdot \sin \left( {\frac{1}{\pi }\left( {x + \pi } \right)} \right)}$

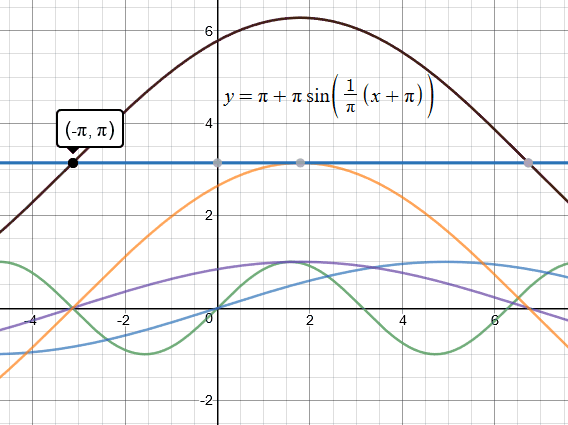
Goniometrische vergelijkingen oplossen

---

Opdracht

1. $
   \sqrt 2  \cdot \sin (2x - \pi ) = 1
   $
   $
   \sin (2x - \pi ) = \frac{1}{2}\sqrt 2
   $
   $
   2x - \pi  = \frac{1}{4}\pi  + k \cdot 2\pi
   $ of $
   2x - \pi  = \frac{3}{4}\pi  + k \cdot 2\pi
   $
   $
   2x = 1\frac{1}{4}\pi  + k \cdot 2\pi
   $ of $
   2x = 1\frac{3}{4}\pi  + k \cdot 2\pi
   $
   $
   x = \frac{5}{8}\pi  + k \cdot \pi
   $ of $
   x = \frac{7}{8}\pi  + k \cdot \pi
   $
2. $
   2\cos \left( {2x - \frac{1}{3}\pi } \right) = \sqrt 3
   $
   $
   \cos \left( {2x - \frac{1}{3}\pi } \right) = \frac{1}{2}\sqrt 3
   $
   $
   2x - \frac{1}{3}\pi  = \frac{1}{6}\pi  + k \cdot 2\pi
   $ of $
   2x - \frac{1}{3}\pi  =  - \frac{1}{6}\pi  + k \cdot 2\pi
   $
   $
   2x = \frac{1}{2}\pi  + k \cdot 2\pi
   $ of $
   2x = \frac{1}{6}\pi  + k \cdot 2\pi
   $
   $
   x = \frac{1}{4}\pi  + k \cdot \pi
   $ of $
   x = \frac{1}{{12}}\pi  + k \cdot \pi
   $
3. $
   \sin (x)\cos (x) - \sin (x) = 0
   $
   $
   \sin (x)\left( {\cos (x) - 1} \right) = 0
   $
   $
   \sin (x) = 0
   $ of $
   \cos (x) - 1 = 0
   $
   $
   x = k \cdot \pi
   $ of $
   \cos (x) = 1
   $
   $
   x = k \cdot \pi
   $ of $
   x = \frac{1}{2}\pi  + k \cdot \pi
   $
   $
   x = k \cdot \frac{1}{2}\pi
   $
4. $
   \sin ^2 (x) = \frac{1}{2}
   $
   $
   \sin (x) =  - \sqrt {\frac{1}{2}}
   $ of $
   \sin (x) = \sqrt {\frac{1}{2}}
   $
   $
   \sin (x) =  - \frac{1}{2}\sqrt 2
   $ of $
   \sin (x) = \frac{1}{2}\sqrt 2
   $
   $
   x = 1\frac{1}{4}\pi  + k \cdot 2\pi
   $ of $
   x = 1\frac{3}{4}\pi  + k \cdot 2\pi
   $ of $
   x = \frac{1}{4}\pi  + k \cdot 2\pi
   $ of $
   x = \frac{3}{4}\pi  + k \cdot 2\pi
   $
   $
   x = \frac{1}{4}\pi  + k \cdot \frac{1}{2}\pi
   $

Toepassingen en probleemaanpak

---

Opdracht 1

• $\eqalign{h = 22 + 20 \cdot \sin \left( {\frac{{2\pi }}{{60}}t} \right)}$

Opdracht 2

• De evenwichtslijn: $a=\frac{25+9}{2}=17$
• De amplitude: $b=25-17=8$
• De periode is 365 dagen. Dus $c=\frac{2\pi}{365}$
• 'Stijgend door de evenwichtsstand' op 91 dagen voor $T_{max}$.
  $d=201-91=110$

...finito...!

De formule:

• $
  \eqalign{T = 17 + 8 \cdot \sin \left( {\frac{{2\pi }}{{365}}\left( {n - 110} \right)} \right)}
  $

Opdracht 3

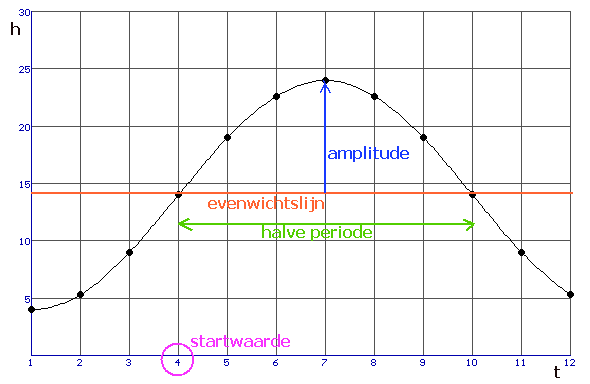
Bij benadering:

• $a=14$
• $b=10$
• $\eqalign{c=\frac{2\pi}{12}}$
• $d=4$

De formule wordt:

$
\eqalign{h(t) = 14 + 10\sin \left( {\frac{{2\pi }}{{12}}\left( {t - 4} \right)} \right)}
$

©2004-2024 W.v.Ravenstein