bladzijde 118

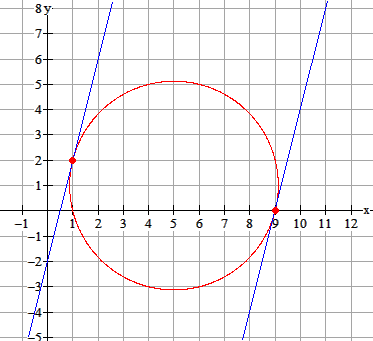
Schrijf de vergelijking van de cirkel om in 'de andere notatie':

$\eqalign{
  & {\left( {x - 5} \right)^2} + {(y - 1)^2} = 17  \cr
  & {x^2} - 10x + 25 + {y^2} - 2y + 1 = 17  \cr
  & {x^2} + {y^2} - 10x - 2y + 9 = 0 \cr} $

Vul $y=4x+q$ in de vergelijking in:

$\eqalign{
  & {x^2} + {\left( {4x + q} \right)^2} - 10x - 2(4x + q) + 9 = 0  \cr
  & {x^2} + 16{x^2} + 8qx + {q^2} - 10x - 8x - 2q + 9 = 0  \cr
  & 17{x^2} + 8qx - 18x + {q^2} - 2q + 9 = 0 \cr} $

Omdat het om de raaklijn gaat  heeft deze vergelijking 1 oplossing. In dat geval is de discriminant nul. Bepaal $a$, $b$ en $c$, bereken $D=b^2-4ac$ en neem $D=0$:

$\eqalign{
  & 17{x^2} + (8q - 18)x + ({q^2} - 2q + 9) = 0  \cr
  & a = 17,\,\,b = 8q - 18\,\,en\,\,c = {q^2} - 2q + 9  \cr
  & D = {\left( {8q - 18} \right)^2} - 4 \cdot 17\left( {{q^2} - 2q + 9} \right)  \cr} $

Neem $D=0$ en los de vergelijking op om de mogelijke waarde(n) van $q$ te bepalen:

$\eqalign{
  & 64{q^2} - 288q + 324 - 68{q^2} + 136q - 612 = 0  \cr
  &  - 4{q^2} - 152q - 288 = 0  \cr
  & {q^2} + 38q + 72 = 0  \cr
  & (q + 36)(q + 2) = 0  \cr
  & q =  - 36 \vee q =  - 2 \cr} $

©2004-2024 W.v.Ravenstein