|
Raaklijnen aan cirkels
Werkschema voor het opstellen van een vergelijking van een raaklijn $k$ aan de cirkel $c$ met middelpunt $M$ in een gegeven punt $A$ op $c$.
-
Bereken de richtingscoëfficiënt $rc_l$ van de lijn $l$ door $M$ en $A$
-
Gebruik $k\perp l$, dus $rc_k·rc_l=-1$, om de richtingscoëfficiënt $rc_k$ van $k$ te berekenen.
-
Gebruik $rc_k$ en de coördinaten van $A$ om een vergelijking van $k$ op te stellen.
Voorbeeld
Gegeven is de cirkel $c:x^2+y^2-6x-2y+5=0$. De punten $A$ en $B$ met $x_A=x_B=2$ en $y_A\gt y_B$ liggen op $c$. De lijn $k$ raakt $c$ in $A$ en de lijn $l$ raakt $c$ in $B$.
-
Stel van $k$ en van $l$ een vergelijking op.
Uitwerking
|
Snijpunten van lijnen met cirkels
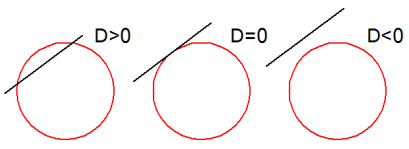
Ontstaat na substitutie van $y=ax+b$ in de cirkelvergelijking een tweedegraadsvergelijking waarvan de discriminant
-
groter dan nul, dan zijn er twee snijpunten
-
kleiner dan nul, dan zijn er geen snijpunten
-
gelijk aan nul, dan raakt de lijn de cirkel
Voorbeeld
Gegeven is de cirkel $c:(x-5)^2+(y-1)^2=17$.
-
Bereken voor welke waarde van $q$ de lijn $y=4x+q$ de cirkel raakt.
Uitwerking
|
raaklijnen en snijpunten bij cirkels