HAVO wiskunde B - logaritmische functie

Opgave

Gegeven: $
f(x) = {}^2\log (x^2  - 4x)
$.

1. Plot de grafiek.
2. Heeft de grafiek asymptoten? Zo ja, geef de vergelijking(en).
3. Heeft f een inverse (leg uit)
4. Bereken de snijpunten van f met de x-as.
5. Laat zien dat de grafiek symmetrisch is in de lijn x=2.

Uitwerking

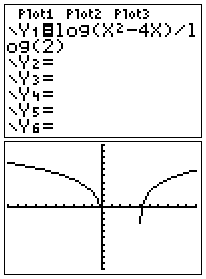
1. Gedaan! (zie plaatje rechts)
2. Ja, bij x=0 en x=4
   $
   \eqalign{
     & x^2  - 4x = 0  \cr
     & x\left( {x - 4} \right) = 0  \cr
     & x = 0\,\,of\,\,x = 4 \cr}
   $
3. Nee, voor sommige waarden van 'y' zijn er meerdere waarden voor 'x' mogelijk.
4. Dat zijn de punten $(2-\sqrt{5}, 0)$ en $(2+\sqrt{5}, 0)$
   $
   \eqalign{
     & {}^2\log (x^2  - 4x) = 0  \cr
     & x^2  - 4x = 1  \cr
     & x^2  - 4x - 1 = 0  \cr
     & (x - 2)^2  - 4 - 1 = 0  \cr
     & (x - 2)^2  = 5  \cr
     & x = 2 \pm \sqrt 5  \cr}
   $
5. Je moet laten zien dat f(2-p)=f(2+p) voor alle waarden van p (voor het domein).
   $
   \eqalign{
     & f(2 - p) = f(2 + p)  \cr
     & {}^2\log (\left( {2 - p} \right)^2  - 4(2 - p) = {}^2\log (\left( {2 + p} \right)^2  - 4(2 + p)  \cr
     & {}^2\log (4 - 4p + p^2  - 8 + 4p) = {}^2\log (4 + 4p + p^2  - 8 - 4p)  \cr
     & {}^2\log (p^2  - 4) = {}^2\log (p^2  - 4) \cr}
   $

©2004-2024 W.v.Ravenstein