Examenvraagstuk VMBO

ACHTVLAKDOBBELSTENEN

q675img2.gif Roy gooit één keer met twee achtvlakdobbelstenen, een rode en een blauwe. Dit noemt hij een worp. Daarna telt hij de getallen van de bovenliggende vlakken bij elkaar op. In de situatie op de foto heeft hij in één worp bij elkaar tien gegooid. De acht vlakken met de getallen 1, 2, 3, 4, 5, 6, 7 en 8 hebben ieder evenveel kans om boven te komen. Roy kan op vier verschillende manieren in één worp bij elkaar vijf gooien.

  1. Schrijf deze vier manieren op.

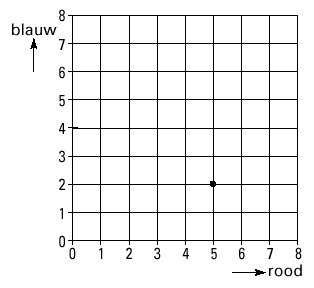
Eén van de mogelijke worpen is (5, 2). Dit betekent dat Roy met de rode dobbelsteen vijf heeft gegooid en met de blauwe twee. In het rooster hieronder is die worp door een punt aangegeven. In de uitwerkbijlage bij vraag 2 is een rooster getekend.

q675img1.gif

Roy gooit in één worp bij elkaar acht.

  1. Geef in het rooster in de uitwerkbijlage bij vraag 2 alle mogelijke worpen met bij elkaar acht aan.

Roy gooit 320 keer met de twee achtvlakdobbelstenen.

  1. Hoeveel keer verwacht je dat hij bij elkaar zes gooit? Laat zien hoe je aan je antwoord komt. Je mag het rooster in de uitwerkbijlage bij vraag 3 gebruiken.

Roy en Bas besluiten een spel te gaan spelen. Ze noemen het: “Wie het hoogste getal gooit”. Roy gooit met de rode achtvlakdobbelsteen en Bas met de blauwe. Wie het hoogste getal gooit, wint. Bij gelijke getallen wint niemand. Ze spelen het spel 480 keer.

  1. Hoeveel keer verwacht je dat Bas zal winnen? Leg uit hoe je aan je antwoord bent gekomen. Je mag het rooster in de uitwerkbijlage bij vraag 4 gebruiken.

Roy pakt een andere rode achtvlakdobbelsteen; dit is een valse achtvlakdobbelsteen. Met deze achtvlakdobbelstenen gooit hij altijd zeven. Roy beweert dat hij ongeveer 75% van de spelletjes waarbij hij met de valse achtvlakdobbelsteen gooit, zal winnen.

  1. Laat zien dat Roy gelijk heeft. Schrijf je uitleg op.

Examenopgaven VMBO-GL en TL 2004 tijdvak 1