5. de parabool y=a(x-p)²+q
Verticaal verschuiven
Je kunt de grafiek van een functie verticaal verschuiven door bij het functievoorschrift een getal op te tellen of af trekken.
Voorbeeld
Gegeven is $f(x)=x^2-4x-1$. Als je nu 3 optelt bij $f$ dan krijg je $g(x)=x^2-4x+2$. In de tekening zie je dat je $f$ drie omhoog moet verschuiven om $g$ te krijgen.
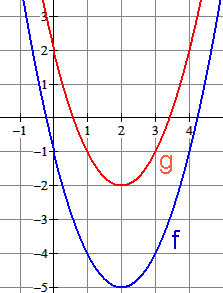
Horizontaal verschuiven
Als je de grafiek van een functie naar links of rechts wilt verschuiven dan verander je in het functievoorschrift de variabele $x$ door $x-p$. De grafiek verschuift dan $p$ naar rechts.
Voorbeeld
Gegeven is $f(x)=x^2-4x-1$. Als je nu in het functievoorschrift van $f$ de variabele $x$ vervangt door $x+3$ dan schuift de grafiek 3 naar links.
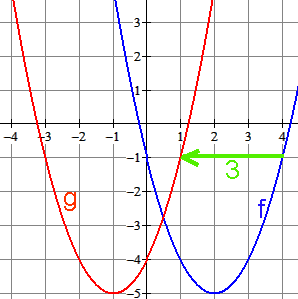
Je krijgt:
- $g(x)=(x+3)^2-4(x+3)-1$
- $g(x)=x^2+6x+9-4x-12-1$
- $g(x)=x^2+2x-4$
Het lijkt (misschien) niet helemaal logisch dat $x-p$ dan $p$ naar rechts is maar als je er over nadenkt dan klopt het wel. Door van $x$ bijvoorbeeld $2$ af te trekken duurt het langer voordat $x$ de waarde krijgt die $x$ eerst had... dus schuift de grafiek naar $2$ naar rechts.
De top van de parabool y=a(x-p)2+q
De top van de parabool $y=a(x-p)^2+q$ is het punt $(p,q)$.
Voorbeeld
Gegeven: $f(x)=\frac{1}{2}(x-3)^2+2$.
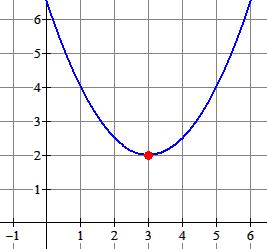
- De top is het punt $(3,2)$.
Hoe zit dat?
De parabool $f(x)=\frac{1}{2}x^2$ heeft als top $(0,0)$. Als je de grafiek 3 naar rechts verschuift en 2 omhoog dan verander je het functievoorschrift van $f$ zo:
- Vervang $x$ door $x-3$
- Tel er 2 bij op
Je krijgt $f(x)=\frac{1}{2}(x-3)^2+2$.
Voorbeelden
Geef de coördinaten van de top van:
- $y=2(x-4)^{2}+4$
- $y=-(x+3)^{2}-11$
- $y=-\frac{2}{3}(x+1\frac{1}{2})^{2}+2\frac{3}{4}$
- $y=x^{2}+3$
- $y=(x+7)^{2}$
Zie antwoorden