3. raaklijnen
Snelheid en richtingscoëfficiënt
In een tijd-afstandgrafiek is de snelheid op $t=a$ gelijk aan de richtingscoëfficiënt van de raaklijn van de grafiek in het bijbehorende punt.
Voorbeeld
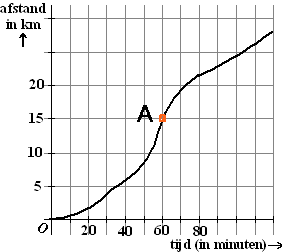
- Geef een schatting van snelheid in km/uur in het punt $A$.
Zie uitgewerkt
Raaklijn en richtingscoëfficiënt
Voor de richtingscoëfficiënt van de raaklijn in het punt $A$ bestaat de notatie:
$
\eqalign{\left[ {{{dy} \over {dx}}} \right]_{x = x_A }}
$
$
\eqalign{\left[ {{{dy} \over {dx}}} \right]_{x = x_A }}
$ is:
- de richtingscoëfficiënt van de raaklijn van de grafiek in $A$
- de helling van de grafiek in $A$
- de snelheid waarmee $y$ verandert voor $x=x_A$
Grafische rekenmachine
De GR bevat een optie om bij een gegeven formule $
\eqalign{\left[ {{{dy} \over {dx}}} \right]_{x = x_A }}
$ te berekenen:
Voorbeeld
De lijn $k$ raakt de grafiek van $f(x)=x^2-2x-1$ in het punt $A$ met $x_A=3$.
- Stel een formule op van $k$
Uitwerking
Bereken met je GR $
\eqalign{\left[ {{{dy} \over {dx}}} \right]_{x =3}=4}
$
De raaklijn wordt $y=4x+b$. Met $f(3)=2$ moet dan gelden dat:
$4·3+b=2$
$12+b=2$
$c=-10$
$k: y=4x-10$
Denkactiviteit:-)
Teken een tijd-afstandgrafiek met op de horizontale as de tijd $t$ in seconden en op de verticale as de afstand $s$ in meter waarbij het volgende geldt:
- op $[0,5]$ is de gemiddelde snelheid 20 m/s
- op $t=5$ is de snelheid 20 m/s
- op $[0,8]$ is de gemiddelde snelheid 15 m/s
- op $t=8$ is de snelheid 15 m/s
getal en ruimte HAVO wiskunde B deel 1 - blz. 84
- zelf doen:-)