4. doorsneden en oppervlakten
De oppervlakte van een doorsnede
Is de ligging van een doorsnede bekend in een ruimtefiguur, waarvan de afmetingen zijn gegeven, dan is vaak de oppervlakte van de doorsnede te berekenen.
Voorbeeld
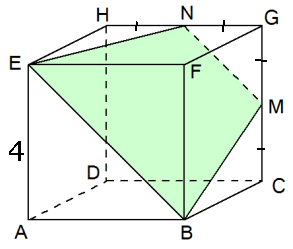
Gegeven de kubus $ABCD.EFGH$ met ribbe 4. $M$ ligt op 't midden van $CG$ en $N$ ligt op 't midden van $GH$.
- Bereken de oppervlakte van de doorsnede $EBMN$.
Uitwerking
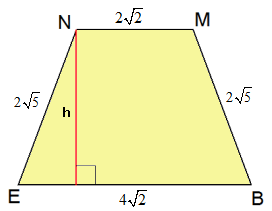
De doorsnede $EBMN$ is een symmetrisch trapezium.
$
h = \sqrt {\left( {2\sqrt 5 } \right)^2 - \left( {\sqrt 2 } \right)^2 } = 3\sqrt 2
$
$\eqalign{O_{trapezium}=\frac{a+b}{2}·h}$
$\eqalign{O_{trapezium}=\frac{4\sqrt{2}+2\sqrt{2}}{2}·3\sqrt{2}}=18$
De oppervlakte van $EBMN$ is 18.
Op ware grootte tekenen
In parallelprojectie worden doorsneden (meestal) niet in hun werkelijke vorm weergegeven. Er treedt vertekening op. Om een goed beeld te krijgen van een doorsnede willen we nog wel 's de doorsnede op ware grootte tekenen.
Met behulp van je geodriehoek en je passer kan je de vlakke figuren in een lichaam in de juiste vorm op papier zetten. In het boek staat daar een mooi voorbeeld van.
Voorbeeld
Bij het op ware grootte tekenen van een doorsnede ga je uit van de grensvlakken waarin de zijden van de doorsnede liggen.
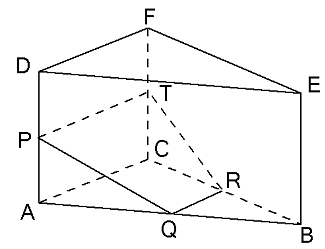
In het rechte prisma ABC.DEF ligt P op het midden van AD, Q op het midden van AB, R op het midden van BC en T op het midden van CF. Hoek BCA is recht, BC = BE = 4 en AC = 3.
- Teken doorsnede PQRT op ware grootte.
Uitwerking
$\angle$PTR en $\angle$TRQ zijn recht.
TP=$3$, TR=$\sqrt{8}$ en QR=$1,5$ (gelijkvormigheid).