0. voorkennis
Letterrekenen
Regels:
- $a(b+c)=ab+ac$
- $(a+b)c=ac+bc$
- $(a+b)(c+d)=ac+ad+bc+bd$
Vergelijkingen oplossen
Je lost een vergelijking op door hem stap voor stap eenvoudiger te maken. Je kunt daarbij:
- termen van het ene lid naar het andere lid brengen
- beide leden door hetzelfde getal te delen of te vermenigvuldigen
Als er in een vergelijking haakjes staan dan is het soms handig om eerst de haakjes weg te werken.
Bij het oplossen van vergelijkingen met breuken kan het handig zijn om eerst de breuken weg te werken.
De formule van een lijn opstellen
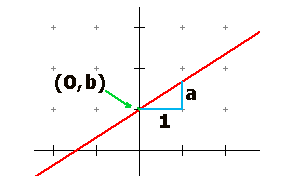De algemene vorm van een lineaire formule is:
- $y=ax+b$
Hierbij is $a$ de richtingscoëfficiënt en $(0,b)$ is het snijpunt met de $y$-as.
Werkschema
Bereken $\eqalign{a=\frac{verticaal}{horizontaal}}$
Bepaal het snijpunt $(0,b)$ met de $y$-as.
- De formule is $y=ax+b$
Opdracht 1
Schrijf zonder haakjes:
$
\begin{array}{l}
a.\,\,\,x(x + 3) = \\
b.\,\,\,5\left( {2x - 11} \right) = \\
c.\,\,\,(4 - x) \cdot x^2 = \\
d.\,\,\,(2x - 1)(x + 4) = \\
\end{array}
$
Opdracht 2
Los op :
$
\begin{array}{l}
a.\,\,\,12x + 3 = 9x + 21 \\
b.\,\,\,2(x - 3) = 10 + 4(2x - 1) \\
c.\,\,\,\frac{1}{4}x + 1 = \frac{2}{3}x - 2 \\
d.\,\,\, - 1\frac{1}{3}x + 3 = 0 \\
\end{array}
$
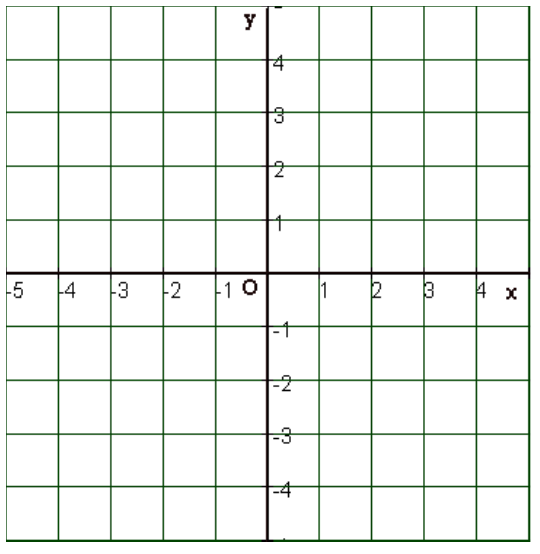
Opdracht 3
Teken in het assenstelsel hieronder de grafieken van :
$l: y=2x-3$
$m: y=-3x+4$
$n: y=\frac{1}{2}x-1$
$p: y=-1\frac{1}{3}x+3$
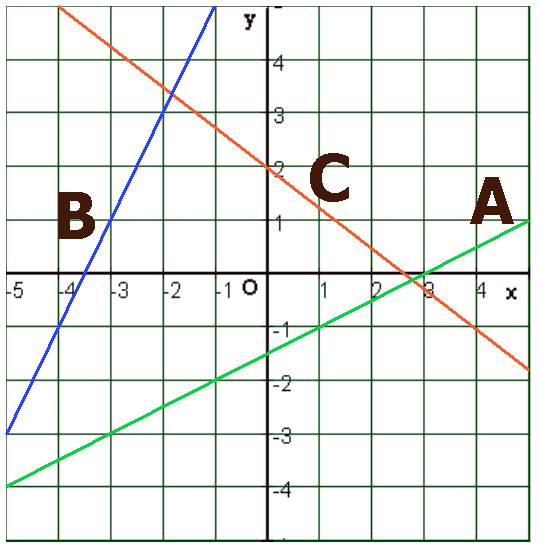
Opdracht 4
Geef steeds een formule bij de grafieken A, B en C in de tekening hiernaast.
Opdracht 1 uitwerking
$
\begin{array}{l}
a.\,\,\,x(x + 3) = x^2 + 3x \\
b.\,\,\,5(2x - 11) = 10x - 55 \\
c.\,\,\,(4 - x) \cdot x^2 = 4x^2 - x^3 \\
d.\,\,\,(2x - 1)(x + 4) = 2x^2 + 8x - x - 4 = 2x^2 + 7x - 4 \\
\end{array}
$
Opdracht 2 uitwerking
-
$
12x + 3 = 9x + 21
$
$
\begin{array}{l}
3x = 18 \\
x = 6 \\
\end{array}
$ -
$
2(x - 3) = 10 + 4(2x - 1)
$
$
\begin{array}{l}
2x - 6 = 10 + 8x - 4 \\
- 6x = 12 \\
x = - 2 \\
\end{array}
$ -
$
\frac{1}{4}x + 1 = \frac{2}{3}x - 2
$
$
\begin{array}{l}
3x + 12 = 8x - 24 \\
- 5x = - 36 \\
x = 7\frac{1}{5} \\
\end{array}
$ -
$
- 1\frac{1}{3}x + 3 = 0
$
$
\begin{array}{l}
- 4x + 9 = 0 \\
- 4x = - 9 \\
x = 2\frac{1}{4} \\
\end{array}
$
Opdracht 3 uitwerking
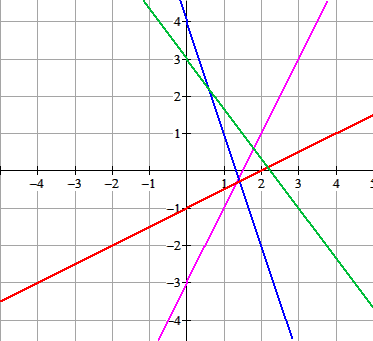
Opdracht 4 uitwerking
$
\begin{array}{l}
A.\,\,\,y = \frac{1}{2}x - 1\frac{1}{2} \\
B.\,\,\,y = 2x + 7 \\
C.\,\,\,y = - \frac{3}{4}x + 2 \\
\end{array}
$