1. lineaire formules
Lineaire formules
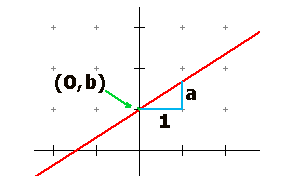Bij een lineair verband tussen $x$ en $y$ hoort als grafiek een rechte lijn. De bijbehoorden formule heeft de vorm:
$y=ax+b$.
Hierin is $a$ de richtingscoëfficiënt.
Het sijpunt van de lijn met de y-as is het punt (0,b).
Grafiek tekenen bij een lineaire formule
Om de lijn $l:y=-0,5x+2$ te tekenen kan je een tabel malen met twee punten, bijvoorbeeld:
Je kunt ook gebruik maken van het snijpunt met de y-as (0,2) en de richtingscoëfficiënt:
1 naar rechts een half omlaag
2 naar rechts één omlaag
Horizontale en verticale lijnen
De formule $y=3$ hoort bij de horizontale lijn door het punt (0,3). De richtingscoëfficiënt van deze lijn is 0. Je kunt $y=3$ ook schrijven als $y=0\cdot x+3$.
Bij formule $x=2$ hoort de verticale lijn door het punt (2,0).
Lineaire formules opstellen
Je moet in deze paragraaf in de volgende situaties een lineaire formule kunnen opstellen:
- Uit de tekst volgt de richtingscoëfficiën en het snijpunt met de vertciale as
- Je weet een punt van de lijn en je weet de richtingscoëfficiënt
Voorbeeld 1
Een kaars is 25 cm lang. Twee uur na het afsteken is er 10 cm opgebrand. Ga uit van een lineair verband en stel een formule op van de lengte $l$ in cm van de kaars na $t$ uur branden.
Uitwerking
Bij $t=0$ is de lengte $l$ gelijk aan 25. De lengte neemt per uur af met 5 cm. De richtingscoëfficiënt is -5. De formule is:
$l = -5t + 25$
Met $l$ in cm en $t$ in uren.
Voorbeeld 2
De lijn $l$ gaat door het punt $A(10,25)$ en $rc_l=\frac{3}{4}$. Stel een formule op van $l$.
Uitwerking
De formule wordt $y=\frac{3}{4}x+b$. Het punt $A(10,25)$ invullen geeft:
$25=\frac{3}{4}\cdot 10+b$
$25=7,5+b$
$b=17,5$
De formule: $y=\frac{3}{4}x+17,5$
Opdracht 1
Teken de grafieken van de lijnen $k$, $l$, $m$ en $n$ in een assenstelsel:
$k: y = 10x - 40$
$l: y = -12\frac{1}{2}x+50$
$m: y = 30$
$n: x = 10$
Opdracht 2
Aan het wateroppervlak heerst een druk van 1015 hPa. Onder water neemt de druk per 10 meter met 1000 hPa toe.
- Stel een formule op van de druk $P$ in hPa op een diepte van $a$ meter.
Opdracht 3
Een parachutist opent zijn parachute op een hoogte van 600 meter en daalt met een snelheid van 18 km/uur.
- Stel een formule op van de hoogte $h$ in meter $t$ seconden na het openen van de parachute.
Opdracht 4
Gegeven is het lineaire verband $K=aq+b$. De richtingscoëffciënt van de bijbehorende lijn is 9. Voor $q=250$ is $K=2760$.
- Stel een formule op voor K.
Opdracht 1 uitwerking
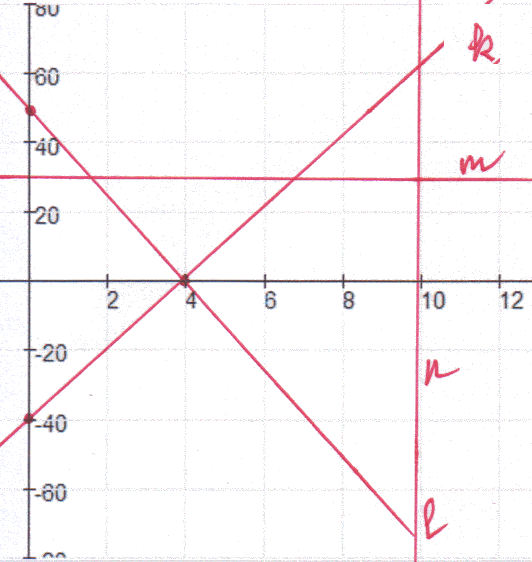
Opdracht 2 uitwerking
De toename per meter is gelijk aan 100 hPa. De richtingscoëffciënt of ook de toename per meter is gelijk aan 100.
De startwaarde is 1015.
De formule: $P=1015+100a$
Opdracht 3 uitwerking
18 km/uur = 18000/3600 m/s = 5 m/s
De afname is -5 meter per seconden. De startwaarde is 600, de formule is:
$h=600-5t$
Opdracht 4 uitwerking
$a=9$, dus $K=9q+b$. Invullen $K=2760$ en $q=250$ geeft:
$2760=9\cdot 250+b$
$2760=2250+b$
$510=b$
$K=9q+510$