2. lineaire formules opstellen
Richtingscoëfficiënt berekenen
De richtingscoëfficiënt is de verticale toename gedeeld door de horizontale toename. Als je de punten $A$ en $B$ hebt dan krijg je:
$rc=\eqalign{\frac{\Delta y}{\Delta x}=\frac{y_B-y_A}{x_B-x_A}}$
Voorbeeld
De lijn $k$ gaat door de punten $P(4,2)$ en $Q(11,5)$. Dan geldt:
$\eqalign{rc_k=\frac{5-2}{11-4}=\frac{3}{7}}$
Bij een exact antwoord laat je breuken staan en ga je niet benaderen. Je moet dan wel de breuken vereenvoudigen als het kan.
Belangrijk daarbij is dat als je boven de
Lineaire formules in de praktijk
Een marktkoopman verkoopt T-shirts. De ervaring leert dat bij een prijs van €5 er per week 90 T-shirts verkocht worden. Bij een prijs van €8 is de weekverkoop nog maar 30 stuks.
Er bestaat een lineair verband tussen de prijs $p$ in euro's van een T-shirt en de weekverkoop $q$.
De formule
Je kunt nu een formule opstellen voor $q=ap+b$ door de punten $A(5,90)$ en $B(8,30)$.
$\eqalign{a=\frac{30-90}{8-5}=\frac{-60}{3}=-20}$
De vergelijking wordt $q=-20p+b$. Invullen van de coördinaten van $A$ geeft:
$90=-20\cdot 5+b$
$90=-100+b$
$190=b$
De formule is: $q=-20p+190$
- Hoeveel is de weekverkoop bij een prijs van €6,95?
Wiskundig model
Een formule waarmee je de werkelijkheid benadert is een voorbeeld van een wiskundig model. Je kunt een model gebruiken om voorspellingen te doen, maar daarbij moet je voorzichtig zijn.
- Voor welk waarden van $x$ geldt de formule?
- Is het wel een lineair verband? Of is dat slechts bij benadering en alleen zinnig op een beperkt domein?
- Klopt de grafiek wel buiten de gegeven meetpunten? Zijn de verbindingen tussen de meetpunten lijnstukken of misschien toch niet?
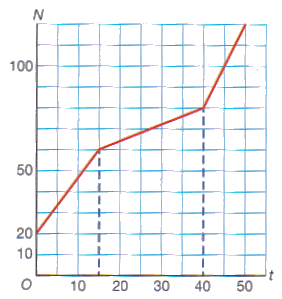
Opdracht 1
- Stel een formule op van de lijn door de punten $A(5,3)$ en $B(25,18)$.
![]()
Opdracht 2
- Stel een formule op voor de lijn door de punten $C(180,360)$ en $D(160,250)$.
Opdracht 3 (A28)
'En hoe ervaart u uw gezondheidstoestand?'. Bij een onderzoek blijkt het percentage $P$ van de mensen dat ontevreden is met de gezondheidstoestand lineair toeneemt met de leeftijd $t$ in jaren. Van de 42-jarigen is een kwart ontevreden en van de 72-jarigen is dat 49%.
- Stel een formule van $P$ op.
- Schat hoeveel procent van de 48-jarigen ontevreden is met zijn gezondheid.
- Er zijn in Nederland ongeveer 225.000 personen van 52 jaar. Schat hoeveel van hen tevreden zijn met hun gezondheid.
- Bereken hoeveel procent van de 10-jarige ontevreden is met zijn gezondheid. Geef commentaar.
![]()
Opdracht 4 (A30)
De organisatiegraad is het percentage werknemers dat lid is van een vakbond. Was de organisatiegraad in Nederland op 1 januari 1999 nog 27%. In de jaren erna nam deze lineair af met 20% op 1 januari 2013.
- Stel de formule op van de organisatiegraad $O$. Neem de tijd $t$ in jaren met $t=0$ op 1 januari 2000.
- Op 1 juli 2007 waren er in Nederland 7,3 miljoen werknemers. Hoeveel van hen waren lid van een vakbond?
- Op 1 januari 2001 waren er 7,0 miljoen werknemers, waarvan er 2,1 miljoen ouder dan 45 jaar waren. Van deze 45-plussers was 31% lid van een vakbond. Hoeveel procent van alle vakbondsleden was op 1 januari 2001 ouder van 45 jaar?
Opdracht 1 uitwerking
De lijn $y=ax+b$ door de punten $A(5,3)$ en $B(25,18)$ geeft:
$\eqalign{a=\frac{18-3}{25-5}=\frac{15}{20}=\frac{3}{4}}$
Invullen van $A(5,3)$ in $y=\frac{3}{4}x+b$ geeft:
$\eqalign{3=\frac{3}{4}\cdot 5+b}$
$\eqalign{3=\frac{15}{4}+b}$
$\eqalign{3=3\frac{3}{4}+b}$
$\eqalign{-\frac{3}{4}=b}$
De formule: $\eqalign{y=\frac{3}{4}x-\frac{3}{4}}$
Opdracht 2 uitwerking
De lijn $y=ax+b$ door de punten $C(180,360)$ en $D(160,250)$ geeft:
$\eqalign{a=\frac{250-360}{160-180}=\frac{-110}{-20}=5\frac{1}{2}}$
Invullen van $C(180,360)$ in $y=5\frac{1}{2}x+b$ geeft:
$360=5\frac{1}{2}\cdot 180+b$
$360=990+b$
$-630=b$
De formule: $y=5\frac{1}{2}x-630$
Opdracht 3 uitwerking
Neem $P=at+b$ met (42,25) en (72,49). Dat geeft:
$\eqalign{a=\frac{49-25}{72-42}=\frac{24}{30}=0,8}$
Invullen van (42,25) geeft $b=-8,6$
- Formule: $P=0,8t-8,6$
- Neem $t=48$ dan $P=29,8\%$
- Neem $t=52$ dan $P=33\%$ ontevreden. $67\%$ van $225.000$ geeft $150.750$ tevreden.
- Neem $t=10$ dan $P=-0,6$ ontevreden. Er zijn meer 10-jarige tevreden met hun gezondheid dan dat er 10-jarige zijn. Kennelijk geldt de formule alleen vanaf een bepaalde leeftijd.
Opdracht 4 uitwerking
-
De organistatiegraad is in 14 jaar met 7% afgenomen. De gemiddelde afname is 0,5% per jaar. Op $t=0$ was de organistatiegraad gelijk aan 26,5%.
Formule: $O=-0,5t+26,5$ in procenten. - Neem $t=7,5$. Dan $O=22,75$. Dat is dan 22,75% van 7.300.000 en dat is 1.660.750 werknemers.
-
Er zijn 26% van 7.000.000 werknemers lid van een vakbond. Dat zijn er 1.820.000.
Er zijn 2.100.000 werknemers ouder dan 45 jaar. Daarvan was 31% lid van een vakbond. Dat zijn 651.000 werknemers.
651.000 van de 1.820.000 is ongeveer 35,8%.
