1. soorten verdelingen
Verdelingen, centrummaten en spreiding
- Voorbeelden van verdelingskrommen.
symmetrische verdeling
- het gemiddelde, de modus en de mediaan vallen samen
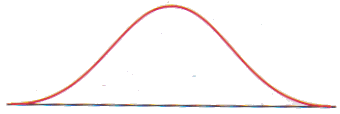
tweetoppige verdeling
- in de figuur hiernaast liggen het gemiddelde en de mediaan tussen te twee toppen
- de standaardafwijking is relatief groot
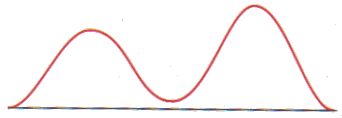
rechts-scheve verdeling
- het gemiddelde en de mediaan liggen rechts van de top
- de staart rechts zorgt voor een relatief grote standaardafwijking
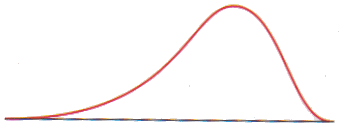
links-scheve verdeling
- het gemiddelde en de mediaan liggen links van de top
- de staart links zorgt voor een relatief grote standaardafwijking
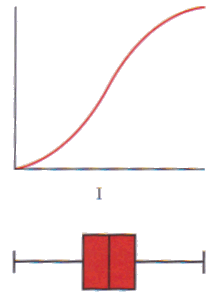
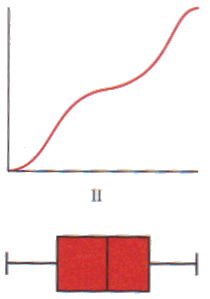
Cumulatieve verdelingskrommen en boxplots
Bij de verdelingen I, II, III en IV hierboven zijn cumulatieve verdelingskrommen en boxplots te schetsen. Omgekeerd kan je uit een cumulatieve verdelingskromme of een boxplot de verdeling herkennen.
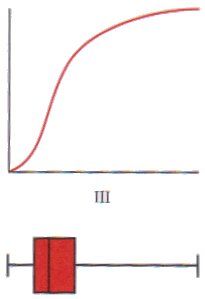
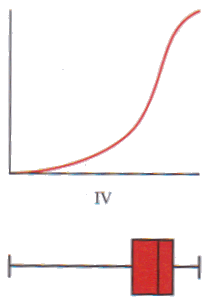
Opdracht 1 (11)
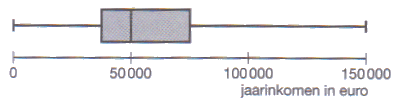
Gegeven de boxplot::
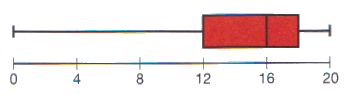
- Schets de bijbehorende verdelingskromme.
- Met wat voor een soort verdeling heb je te maken?
- Hoe ligt het gemiddelde ten opzichte van de mediaan?
Opdracht 2 (A12)

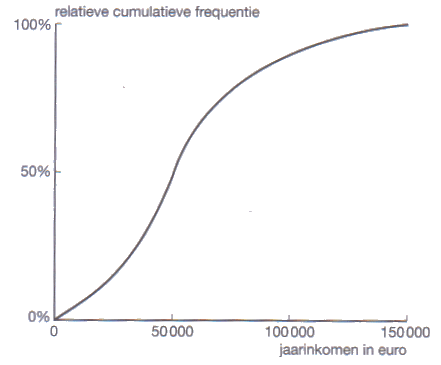
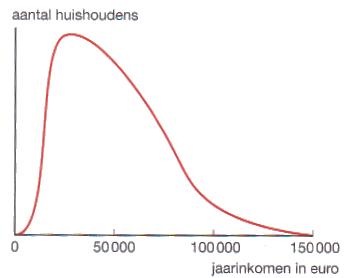
De verdelingskromme geeft informatie over de verdeling van de jaarinkomens van huishoudens in een land.
- Hoe ligt de mediaan ten opzichte van de modus bij deze verdeling?
- Schets de relatieve cumulatieve verdelingskromme.
- Schets de boxplot.
Opdracht 1
- Weinig waarnemingsgetallen aan het begin en veel op het eind

- Het is een links-scheve verdeling
- Het gemiddelde ligt links van de mediaan
Opdracht 2
- De mediaan ligt rechts van de modus
- Het steilste stuk zit ongeveer bij 25.000 euro. De mediaan is ongeveer 50.000