4. wortelfuncties en gebroken functies
Wortelvergelijkingen en algemene vormen
Algemene vormen bij het oplossen van vergelijkingen:
- $A·B=0$ geeft $A=0$ of $B=0$
- $A^2=B^2$ geeft $A=B$ of $A=-B$
- $A·B=A·C$ geeft $A=0 \vee B=C$
- $A·B=A$ geeft $A=0 \vee B=1$
Voorbeeld
$\eqalign{
& (x - 2)\sqrt {x + 10} = {(x - 2)^2} \cr
& (x - 2)\sqrt {x + 10} = (x - 2)(x - 2) \cr
& x - 2 = 0 \vee \sqrt {x + 10} = x - 2 \cr
& ... \cr
& x = 2 \vee x = 6 \cr} $
- Zie ook vormen en nog meer vormen
Functies van de vorm $f(x)=a+b\sqrt{cx+d}$
Als je de grafiek van een wortelfunctie wilt tekenen dan bepaal je eerst het domein en het beginpunt.
De uitdrukking onder het wortelteken moet altijd groter of gelijk aan nul zijn.
Voorbeeld
$
y=2\sqrt{x-4}+5
$
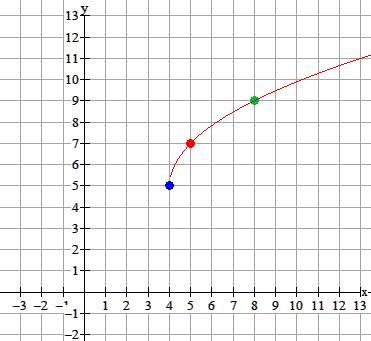
Zie twee grafieken
Functies van de vorm $f(x)=a+\sqrt{-x^2+bx+c}$
De grafiek van $f(x)=2+\sqrt{-x^2+6x+7}$ is een halve cirkel. Dat kan je aantonen door de formule anders te schrijven. Dat gaat zo:
$\eqalign{
& y = 2 + \sqrt { - {x^2} + 6x + 7} \cr
& y - 2 = \sqrt { - {x^2} + 6x + 7} \cr
& {(y - 2)^2} = - {x^2} + 6x + 7 \cr
& {x^2} - 6x + {(y - 2)^2} = 7 \cr
& {(x - 3)^2} - 9 + {(y - 2)^2} = 7 \cr
& {(x - 3)^2} + {(y - 2)^2} = 16 \cr} $
Dat is een cirkel met middelpunt $M(3,2)$ en de straal $r=4$.
Bij de oorspronkelijke formule is $f(x)\ge2$ zodat alleen de bovenste helft van de cirkel bij de formule hoort.
Functies van de vorm $\eqalign{f(x)=\frac{ax+b}{cx+d}}$
Een gebroken lineaire functie is van de vorm:
- $\eqalign{f(x)=\frac{ax+b}{cx+d}}$
Elke gebroken lineaire functie kan je opvatten als het resultaat van transformaties van de standaardfunctie $\eqalign{f(x)=\frac{1}{x}}$.
De grafiek is een hyperbool en heeft een verticale en horizontale asymptoot.
Asymptoten bij gebroken functies
- De verticale asymptoot kan je vinden door de noemer gelijk aan 0 te stellen.
- Beredeneer wat de functiewaarde wordt voor grote waarden van $x$.
Voorbeeld
Gegeven is de functie $\eqalign{f(x)=\frac{4x+3}{2x-3}}$.
- Schets de grafiek van $f$.
- Los algebraisch op $f(x)\le\frac{2}{3}x+3$
- Druk $x$ uit in $y$.
Pagina 131 van je boek.
Afspraak
Bij het tekenen of schetsen van de grafiek van een gebroken functie stel je eerst de formules op van de asymptoten. Je tekent de asymptoten als stippellijnen in de figuur en zet de formules erbij.