Gebroken functie
n een gebroken functie komt de variabele in de noemer van een breuk voor.
De eenvoudigste gebroken functie is $\eqalign{f(x)=\frac{1}{x}}$. De functie is een standaardfunctie. De grafiek van deze functie is een standaardgrafiek en heet hyperbool.
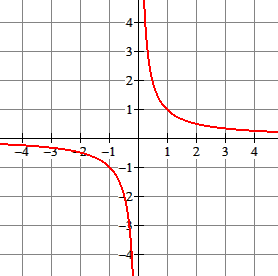
De grafiek bestaat uit twee losse delen. Deze heten de takken van de hyperbool.
Asymptoten
Als je bij $\eqalign{f(x)=\frac{1}{x}}$ voor $x$ een steeds groter getal neemt dan wordt de functiewaarde steeds kleiner. De functiewaarde komt steeds dichter bij y=0 te liggen.
De $x$-as (de lijn y=0) is de horizontale asymptoot van de grafiek van $f$.
Als je voor $x$ getallen neemt die steeds dichter bij 0 liggen dan wordt de functiewaarde steeds groter (of kleiner van de andere kant).
De $y$-as (de lijn x=0) is de verticale asymptoot van de grafiek van $f$.
- Een asymptoot is een lijn waarmee de grafiek op den duur vrijwel samenvalt.
Algemene formule voor een lineaire gebroken functie
- $\eqalign{f(x)=a+\frac{b}{x-c}}$
Asymptoten
- Horizontale asymtoot: $y=2$
- Verticale asymtoot: $x=c$
De waarde van $b$ kan je vinden door een punt van de grafiek in te vullen. Neem een handig punt...:-)
Opgave 17
Gegeven: $\eqalign{f(x)=2+\frac{8}{x+3}}$ en $g(x)=2x+2$.
- Bereken de coördinaten van de snijpunten van $f$ en $g$.
Opgave 18
De grafiek van $\eqalign{f(x)=\frac{1}{x}}$ gaat over in de grafiek van $\eqalign{g(x)=2+\frac{8}{x+3}}$.
- Via welke transformaties is dat mogelijk?
Opgave 19
Gebruik (eventueel) de online rekenmachine of je grafische rekenmachine.
- Geef mogelijke formules die horen bij de volgende grafieken:
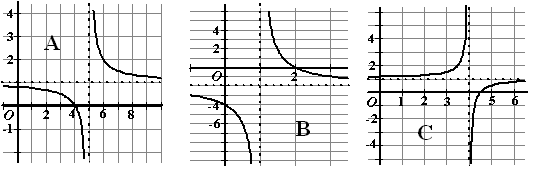
http://www.hhofstede.nl
Gegeven: $\eqalign{f(x)=\frac{2}{x-3}+4}$. Voer de volgende transformaties uit:
- Vermenigvuldig met de factor $2$ t.o.v. de $y$-as
- Verschuif de grafiek $3$ naar links
- Vermenigvuldig met de factor $\frac{1}{2}$ t.o.v. de $x$-as
Geef een formule voor het eindresultaat