J. Jan en Piet
Opgave
Jan en Piet willen elkaar morgen tussen 11.00 en 12.00 uur treffen op het station. Ze spreken af dat ze een kwartier op elkaar zullen wachten en dan weer vertrekken.
- Hoe groot is de kans dat ze elkaar treffen?
Uitwerking
We veronderstellen dat ze elk tussen 11 uur en 12 uur toekomen en dat elke aankomsttijd even waarschijnlijk is. In volgende schets stellen we langs de X-as de aankomsttijd van Jan voor en langs de Y-as die van Piet (beide assen lopen van 11u tot 12u).
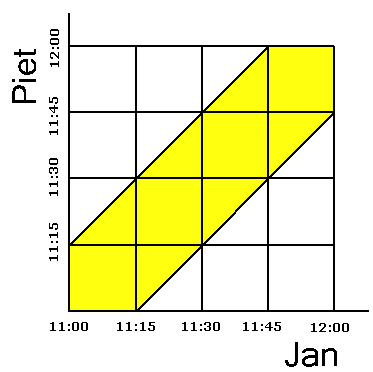
Ze ontmoeten elkaar als hun aankomsttijd hoogstens 15 min uiteenligt. Dit is wanneer hun aankomsttijden een punt voorstellen binnen het gekleurde gebied. Alle punten binnen het vierkant zijn even waarschijnlijk. De kans dat ze elkaar ontmoeten is $\frac{7}{16}$.
Toelichting
Soms denken leerlingen dat kansberekenen vooral een kwestie van op het goede moment het juiste kansmodel uit de kast trekken. Is het een binomiaal kansprobleem? Is het een normale verdeling? Of wat is het? Maar zo werkt dat natuurlijk niet. De verschillende kansmodellen helpen natuurlijk wel om de problemen in kaart te brengen en te bestuderen. Waar zijn er overeenkomsten? Waar zijn de verschillen?
In dit geval is het kansmodel vooral de kans om je doel te raken met het gooien van het pijltje...